题目内容
已知对任意实数x,二次函数f(x)=ax2+bx+c恒非负,且a<b,则
的最小值是
| a+b+c | b-a |
3
3
.分析:由题意可得 b>a>0,再由△≤0得到c≥
,故
≥
=
≥
=3,从而求得
的最小值.
| b2 |
| 4a |
| a+b+c |
| b-a |
a+b+
| ||
| b-a |
| [3a+(b-a)]2 |
| 4a(b-a) |
(2
| ||
| 4a(b-a) |
| a+b+c |
| b-a |
解答:解:∵二次函数f(x)=ax2+bx+c恒非负,故 b>a>0.
再由△≤0得到c≥
.
则
≥
=
=
≥
=
=3,
故当3a=b-a,且 c=
时,
取得最小值是3,
即 b=c=4a时,
的最小值是3,
故答案为 3.
再由△≤0得到c≥
| b2 |
| 4a |
则
| a+b+c |
| b-a |
a+b+
| ||
| b-a |
| 4a2+b2+4ab |
| 4a(b-a) |
| [3a+(b-a)]2 |
| 4a(b-a) |
(2
| ||
| 4a(b-a) |
| 12a(b-a) |
| 4a(b-a) |
故当3a=b-a,且 c=
| b2 |
| 4a |
| a+b+c |
| b-a |
即 b=c=4a时,
| a+b+c |
| b-a |
故答案为 3.
点评:本题主要考查二次函数的性质,基本不等式的应用,式子的变形是解题的关键和难点,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
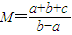 的最小值是 .
的最小值是 .