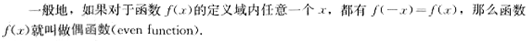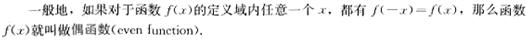题目内容
阅读理解(1)教材27页有如下内容:

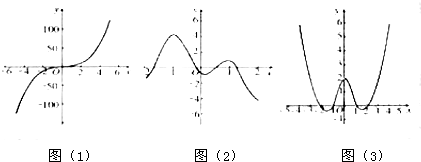
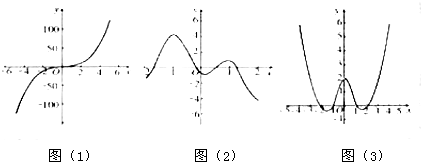
分别观察三个图象,你看出哪些变化规律
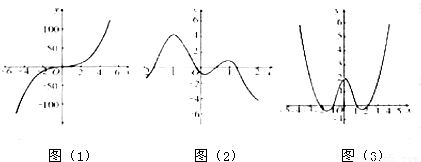
(2)教材是这样定义偶函数的(如图文字)
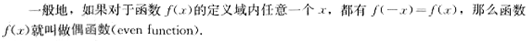
问题1:辅导班的小王认为 f(x)=x2,x∈[-5,5)是偶函数,理由如下:对于函数定义域内的任意一个x,f(-x)=(-x)2=x2=f(x),所以该函数式偶函数,你认为对吗?为什么?
问题2:奇函数的定义是?
【答案】分析:问题1:根据偶函数的定义,须对定义域内任意一个x,都有f(-x)=f(x)成立才为偶函数,要说明不是偶函数,构造反例,只需找一个x满足f(-x)≠f(x)即可.
问题2:类比偶函数定义即可给出奇函数的定义.
解答:问题1:答:该函数式不是偶函数,原因如下:
根据偶函数定义,对定义域内任意一个x,都有f(-x)=f(x),
对于f(x)=x2,x∈[-5,5),当x=-5时,f(-5)≠f(5),因为x=5时没定义,
故该函数不是偶函数.
问题2:答:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数(odd function).
点评:本题考查函数奇偶性的定义,考查学生对奇偶函数定义的深刻理解,准确理解定义是解决该题的关键,本题命题形式比较新颖.
问题2:类比偶函数定义即可给出奇函数的定义.
解答:问题1:答:该函数式不是偶函数,原因如下:
根据偶函数定义,对定义域内任意一个x,都有f(-x)=f(x),
对于f(x)=x2,x∈[-5,5),当x=-5时,f(-5)≠f(5),因为x=5时没定义,
故该函数不是偶函数.
问题2:答:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数(odd function).
点评:本题考查函数奇偶性的定义,考查学生对奇偶函数定义的深刻理解,准确理解定义是解决该题的关键,本题命题形式比较新颖.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目