题目内容
在△ABC中,三边长AB=7,BC=5,AC=6,则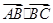 的值为( )
的值为( )
A.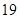 | B.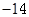 | C.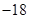 | D.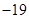 |
A
解析试题分析:根据所给的三角形的三边长度,做出三角形的内角B的余弦,所求的角与两个向量的夹角互补,做出向量的数量积.∵三边长AB=7,BC=5,AC=6,∴cosB= ,
,
∵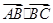 =7×5×(-
=7×5×(- )=-19,故选A.
)=-19,故选A.
考点:本题主要考查平面向量的数量积的运算
点评:本题解题的关键是看清两个向量的夹角,不是三角形的内角二是内角的补角.这一点是个易错点,要引起重视。

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
已知向量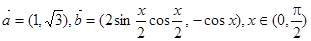 ,若
,若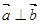 ,则
,则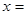
A.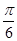 | B.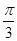 | C.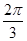 | D.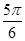 |
已知平面向量 ,且
,且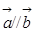 ,则
,则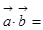 ( )
( )
| A.-30 | B.20 | C.15 | D.0 |
已知向量 ,
, ,若
,若 ∥
∥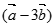 ,则实数k的取值为( )
,则实数k的取值为( )
A. | B. | C. | D. . . |
设向量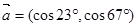 ,
,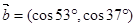 ,
,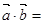 ( )
( )
A.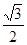 | B.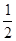 | C.-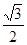 | D.-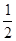 |
已知两个非零向量 满足
满足 ,则下面结论正确
,则下面结论正确
A. | B. | C. | D. |
已知向量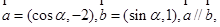 则
则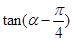 等于( )
等于( )
A.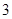 | B.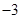 | C. | D.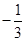 |
已知向量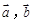 满足
满足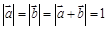 ,则向量
,则向量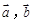 夹角的余弦值为( )
夹角的余弦值为( )
A.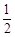 | B. | C.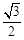 | D.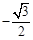 |
设向量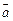 与
与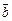 的夹角为
的夹角为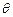 ,定义
,定义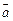 与
与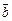 的“向量积”:
的“向量积”: 是一个向量,它的模
是一个向量,它的模 ,若
,若 ,则
,则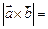
 ( )
( )
A. | B.2 | C.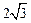 | D.4 |