题目内容
已知函数y=ax的图象经过平面区域
(1)求a取值范围的集合为A;
(2)已知“命题p:?x∈A,使x2+bx+16>0”,写出¬p,若命题p为真命题,求出b取值范围.
|
(1)求a取值范围的集合为A;
(2)已知“命题p:?x∈A,使x2+bx+16>0”,写出¬p,若命题p为真命题,求出b取值范围.
分析:(1)由题意函数y=ax的图象经过平面区域
,画出可行域,利用数形结合的方法进行求解;
(2)根据“命题p:?x∈A,使x2+bx+16>0”,直接写出其否命题,知命题p为真命题,可以等价于x2+bx+16>0在2≤x≤6上有解,然后再利用常数分离法进行求出b的范围;
|
(2)根据“命题p:?x∈A,使x2+bx+16>0”,直接写出其否命题,知命题p为真命题,可以等价于x2+bx+16>0在2≤x≤6上有解,然后再利用常数分离法进行求出b的范围;
解答:解(1)∵函数y=ax的图象经过平面区域
画对可行域:
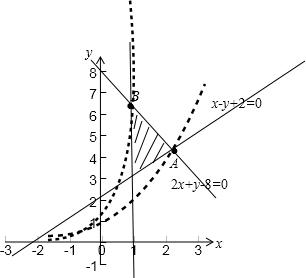
A(2,4),B(1,6)
由图象可知当y=ax经过点A时,a值最小,经过点B时,a值最大,
∴2≤a≤6
∴A={a|2≤a≤6}
(2)?p:?x∈A,使x2+bx+16≤0
命题p:?x∈A,使x2+bx+16>0为真命题
等价于x2+bx+16>0在2≤x≤6上有解
等价于 -b<x+
在2≤x≤6上有解,
只要x+
在[2,6]上的最小值大于-b即可,
∵x+
≥2
=8(当x=4时,等号成立),又f(x)=x+
,其中f(2)=10,f(6)=6+
<10,
∴10≥x+
≥8,要使 -b<x+
在2≤x≤6上有解,
∴-b<10即b>-10;
|
画对可行域:

A(2,4),B(1,6)
由图象可知当y=ax经过点A时,a值最小,经过点B时,a值最大,
∴2≤a≤6
∴A={a|2≤a≤6}
(2)?p:?x∈A,使x2+bx+16≤0
命题p:?x∈A,使x2+bx+16>0为真命题
等价于x2+bx+16>0在2≤x≤6上有解
等价于 -b<x+
| 16 |
| x |
只要x+
| 16 |
| x |
∵x+
| 16 |
| x |
| 16 |
| 16 |
| x |
| 8 |
| 3 |
∴10≥x+
| 16 |
| x |
| 16 |
| x |
∴-b<10即b>-10;
点评:第一问比较简单,利用数形结合的方法画出草图,就可求解,第二问比较麻烦,用到了常数分离法,本题考查的知识点比较全面,是一道综合题;

练习册系列答案
相关题目
