题目内容
(08年安徽卷理) (本小题满分13分)
设椭圆![]() 过点
过点![]() ,且左焦点为
,且左焦点为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于两不同点
相交于两不同点![]() 时,在线段
时,在线段![]() 上取点
上取点![]() ,满足
,满足![]() 。证明:点Q总在某定直线上。
。证明:点Q总在某定直线上。
【解析】本题主要考查直线、椭圆的方程及几何性质、线段的定比分点等基础知识、基本方法和分析问题、解决问题的能力.本小题满分13分.(Ⅰ)由题意: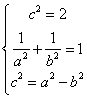 ,解得
,解得![]() .
.
所求的求椭圆![]() 的方程
的方程![]() .
.
(Ⅱ)方法一:设点![]() ,
,![]() ,
,![]() ,由题设,
,由题设,![]() 、
、![]() 、
、![]() 、
、![]() 均不为0,且
均不为0,且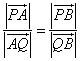 ,又
,又![]() 四点共线,可设
四点共线,可设![]() ,
,![]() ,于是
,于是
![]() ,
,![]() …………………………………①
…………………………………①
![]() ,
,![]() …………………………………②
…………………………………②
由于![]() ,
,![]() 在椭圆上,将①②分别带入
在椭圆上,将①②分别带入![]() 的方程
的方程![]() ,整理得:
,整理得:
![]() ………………③
………………③
![]() ………………④
………………④
由④-③得 ![]() .
.
∵![]() ,∴
,∴![]() .即点
.即点![]() 总在直线
总在直线![]() 上.
上.
方法二:设点![]() ,
,![]() ,
,![]() ,由题设,
,由题设,![]() 、
、![]() 、
、![]() 、
、![]() 均不为0,记
均不为0,记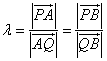 ,则
,则![]() 且
且![]() .
.
又![]() 四点共线,从而
四点共线,从而![]() ,
,![]() ,于是:
,于是:
![]() ,
,![]() ;
;
![]() ,
,![]() .
.
从而![]() ……………①
……………① ![]() ……………②
……………②
又点![]() 在椭圆上,即
在椭圆上,即
![]() ………………③
………………③
![]() ………………④
………………④
①+2![]() ②并结合③,④得
②并结合③,④得![]() ,即点
,即点![]() 总在直线
总在直线![]() 上.
上.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目

 表示的平面区域,则当a从-2连续变化到1时,动直线x+y=a扫过A中的那部分区域的面积为 .
表示的平面区域,则当a从-2连续变化到1时,动直线x+y=a扫过A中的那部分区域的面积为 .