Question

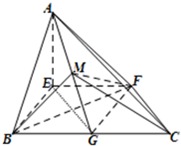直角梯形EFCB中，EF∥BC，EF=BE=

1

2

BC=2，∠BEF=90°，点A是平面BEF外一点，AE⊥面BCFE，且AE=BE，G、M分别是BC、AG的中点．
（1）求证：CF⊥平面BMF；
（2）求三棱锥B-MFG的体积．

Answer 1

分析：（1）连接BF、GE，BF∩GE=0，连接OM，先证CF⊥BF，再证OM⊥CF，由线面垂直的判定定理可证CF⊥平面BMF；
（2）由（1）知，OM⊥平面BFG，即OM为三棱锥M-BGF的高，根据求出OM与底面△BGF的面积，V_B-GMF=V_M-BGF，代入体积公式计算．

解答：解：（1）连接BF、GE，BF∩GE=0，连接OM，
∵EF∥BC，EF=BE=

1

2

BC=2，G是BC的中点，∠BEF=90°，
∴四边形EFGB为正方形，∠BFG=∠GFC=45°，
∴CF⊥BF，
又O，M分别是EG，AG的中点，
∴OM∥AE，∵AE⊥面BCFE，CF?平面BCFE，∴AE⊥CF，
∴OM⊥CF，OM∩BF=O，∴CF⊥平面BMF；
（2）由（1）知，OM⊥平面BFG，OM=

1

2

AE=1，
∴V_B-GMF=V_M-BGF=

1

3

×

1

2

×2×2×1=

2

3

．

点评：本题考查了线面垂直的证明，考查了三棱锥的体积计算，考查了学生的推理论证能力，利用三棱锥的换底性求其体积是常用方法．