题目内容
已知平面区域D由以A(1,3),B(5,2),C(3,1)为顶点的三角形内部以及边界组成.若在区域D上有无穷多个点(x,y)可使目标函数z=x+my取得最小值,则m=( )
| A、-2 | B、-1 | C、1 | D、4 |
分析:将目标函数z=x+my化成斜截式方程后得:y=-
x+
z,若m>0时,目标函数值Z与直线族:y=-
x+
z截距同号,当直线族y=-
x+
z的斜率与直线AC的斜率相等时,目标函数z=x+my取得最小值的最优解有无数多个;若m<0时,目标函数值Z与直线族:y=-
x+
z截距异号,当直线族y=-
x+
z的斜率与直线BC的斜率相等时,目标函数z=x+my取得最小值的最优解有无数多个,但此时是取目标函数取最大值的最优解为无数个,不满足条件.
| 1 |
| m |
| 1 |
| m |
| 1 |
| m |
| 1 |
| m |
| 1 |
| m |
| 1 |
| m |
| 1 |
| m |
| 1 |
| m |
| 1 |
| m |
| 1 |
| m |
解答: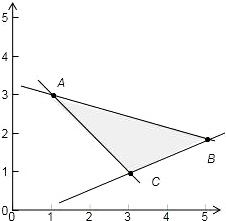 解:依题意,满足已知条件的三角形如下图示:
解:依题意,满足已知条件的三角形如下图示:
令z=0,可得直线x+my=0的斜率为-
,
结合可行域可知当直线x+my=0与直线AC平行时,
线段AC上的任意一点都可使目标函数z=x+my取得最小值,
而直线AC的斜率为
=-1,
所以-
=-1,解得m=1,
故选C.
增加网友的解法,相当巧妙值得体会!请看:
依题意,1+3m=5+2m<3+m,或1+3m=3+m<5+2m,或3+m=5+2m<1+3m
解得 m∈空集,或m=1,或m∈空集,
所以m=1,选C.
评析:此解法妙在理解了在边界处取到最小值这个命题的内蕴,区域的三个顶点中一定有两个顶点的坐标是最优解,故此两点处函数值相等,小于第三个顶点处的目标函数值,本题略去了判断最优解取到位置的判断,用三个不等式概括了三种情况,从而解出参数的范围,此方法可以在此类求参数的题中推广,具有一般性!
 解:依题意,满足已知条件的三角形如下图示:
解:依题意,满足已知条件的三角形如下图示:令z=0,可得直线x+my=0的斜率为-
| 1 |
| m |
结合可行域可知当直线x+my=0与直线AC平行时,
线段AC上的任意一点都可使目标函数z=x+my取得最小值,
而直线AC的斜率为
| 1-3 |
| 3-1 |
所以-
| 1 |
| m |
故选C.
增加网友的解法,相当巧妙值得体会!请看:
依题意,1+3m=5+2m<3+m,或1+3m=3+m<5+2m,或3+m=5+2m<1+3m
解得 m∈空集,或m=1,或m∈空集,
所以m=1,选C.
评析:此解法妙在理解了在边界处取到最小值这个命题的内蕴,区域的三个顶点中一定有两个顶点的坐标是最优解,故此两点处函数值相等,小于第三个顶点处的目标函数值,本题略去了判断最优解取到位置的判断,用三个不等式概括了三种情况,从而解出参数的范围,此方法可以在此类求参数的题中推广,具有一般性!
点评:目标函数的最优解有无数多个,处理方法一般是:①将目标函数的解析式进行变形,化成斜截式;②分析Z与截距的关系,是符号相同,还是相反;③根据分析结果,结合图形做出结论④根据斜率相等求出参数.

练习册系列答案
相关题目
已知平面区域D由以A(1,3),B(5,2),C(3,1)为顶点的三角形内部以及边界组成.若在区域D上有无穷多个点(x,y)可使目标函数z=x+my取得最小值,则m=( )
A.-2
B.-1
C.1
D.4
A.-2
B.-1
C.1
D.4