题目内容
求以抛物线y2=8x的焦点为焦点,且离心率为
的椭圆的标准方程为( )
| 1 |
| 2 |
分析:由题意可得焦点为(2,0),c=2;再由
=
可得a的值,再根据a、b、c的关系求出b的值,即可得到椭圆
的标准方程.
| c |
| a |
| 1 |
| 2 |
的标准方程.
解答:解:由题意可得焦点为(2,0),故c=2.再由
=
可得a=4,∴b=2
.
故椭圆的标准方程为
+
=1.
故选A.
| c |
| a |
| 1 |
| 2 |
| 3 |
故椭圆的标准方程为
| x2 |
| 16 |
| y2 |
| 12 |
故选A.
点评:本题主要考查抛物线和椭圆的标准方程,以及简单性质的应用,属于基础题.

练习册系列答案
相关题目
 的椭圆的标准方程为
的椭圆的标准方程为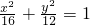
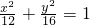

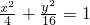
 的椭圆的标准方程为( )
的椭圆的标准方程为( )


