题目内容
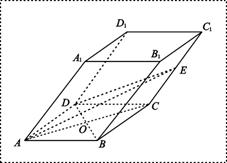
在斜四棱柱![]() 中,已知底面
中,已知底面![]() 是边长为4的菱形,
是边长为4的菱形,![]() ,且点
,且点![]() 在面
在面![]() 上的射影是底面对角线
上的射影是底面对角线![]() 与AC的交点O,设点E是
与AC的交点O,设点E是![]() 的中点,
的中点,![]() .
. ![]()
![]()
(Ⅰ) 求证:四边形![]() 是矩形;
是矩形;
(Ⅱ) 求二面角![]() 的大小;
的大小;
(Ⅲ) 求四面体![]() 的体积.
的体积.
(1)证明略(2)二面角E─BD─C的大小为![]() (3)
(3)![]()
解析:
解法一:(Ⅰ) 连接![]() . 因为四边形
. 因为四边形![]() 为菱形,
为菱形,
所以![]() ,又
,又![]() 面
面![]() ,
,
所以![]() . 而
. 而![]() ,所以
,所以![]() .
.
因为四边形![]() 是平行四边形,所以四边形
是平行四边形,所以四边形![]() 是矩形. 4分
是矩形. 4分
(Ⅱ) 连接OE,因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
∴ ![]() ,即
,即![]() 为二面角E─
为二面角E─![]() ─C的平面角.
─C的平面角.
在菱形![]() 中,
中,![]()
又E是![]() 的中点,
的中点,![]() .所以
.所以![]() .
.
在![]() △
△![]() 中,
中,![]() ,
,
∴ ![]() ,
,![]() ,
,
所以在△![]() 中,有
中,有![]() ,即二面角E─BD─C的大小为
,即二面角E─BD─C的大小为![]() . 9分
. 9分
(Ⅲ) 设点D到平面![]() 的距离为h,则有
的距离为h,则有![]() .
.
因为![]() 是
是![]() 的中点,所以
的中点,所以![]()
![]() 14分
14分
解法二:(Ⅰ) 连结AC、BD相交于O,连结![]() .
.
由已知,有AC⊥BD,![]() ⊥面ABCD,故可建立空间直角坐标系
⊥面ABCD,故可建立空间直角坐标系![]() ,
,
且以下各点的坐标分别为:
![]() , 1分
, 1分
设![]() ,
,
![]()
![]() ,
,
![]() . 3分
. 3分
又![]()
![]()
![]() ,
, ![]() 四边形
四边形![]() 为平行四边形.
为平行四边形.
![]() 是矩形. 4分
是矩形. 4分
(Ⅱ) 设![]() ,则
,则![]() .
.
![]() , 由
, 由![]() 可求得
可求得![]()
![]()
![]()
∴![]() .
.
设![]() 为平面EBD的法向量,
为平面EBD的法向量,
则由![]() ,得
,得![]()
![]() 可取
可取![]()
![]() ,
,
![]() . 6分
. 6分
![]() 平面
平面![]() 平面BDC的法向量为
平面BDC的法向量为![]() ,
,
而 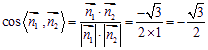 .
.
∴ 二面角E─BD─C的大小为![]() . 9分
. 9分
(Ⅲ) 设![]() 为平面
为平面![]() 的法向量,
的法向量,
则由![]() ,
,
得![]()
![]()
![]()
∴ 可取![]() ,
,![]() .
.
![]() 到平面
到平面![]() 的距离
的距离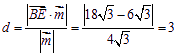 . 11分
. 11分
而![]() ,又由(Ⅰ)知,
,又由(Ⅰ)知,![]() ,
,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
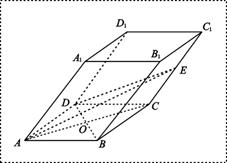 (Ⅲ) 求四面体
(Ⅲ) 求四面体