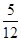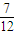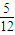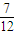题目内容
先后连掷两次骰子分别得到点数m,n,则向量(m,n)与向量(-1,1)的夹角θ>90°的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:掷两次骰子分别得到的点数m,n,组成的向量(m,n)个数为36个,与向量(-1,1)的夹角θ>90°的这个事件包含的基本事件数须将其满足的条件进行转化,再进行研究
解答:解:后连掷两次骰子分别得到点数m,n,所组成的向量(m,n)的个数共有36种
由于向量(m,n)与向量(-1,1)的夹角θ>90°的
∴(m,n)•(-1,1)<0,即m-n>0,满足题意的情况如下
当m=2时,n=1;
当m=3时,n=1,2;
当m=4时,n=1,2,3;
当m=5时,n=1,2,3,4;
当m=6时,n=1,2,3,4,5;
共有15种
故所求事件的概率是
=
故选D
由于向量(m,n)与向量(-1,1)的夹角θ>90°的
∴(m,n)•(-1,1)<0,即m-n>0,满足题意的情况如下
当m=2时,n=1;
当m=3时,n=1,2;
当m=4时,n=1,2,3;
当m=5时,n=1,2,3,4;
当m=6时,n=1,2,3,4,5;
共有15种
故所求事件的概率是
| 15 |
| 36 |
| 5 |
| 12 |
故选D
点评:本题考查等可能事件的概率,考查了概率与向量相结合,以及分类计数的技巧,有一定的综合性.

练习册系列答案
相关题目
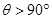 的概率是( )
的概率是( )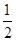 B.
B.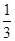 C.
C.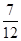 D.
D.