题目内容
已知向量 ,
,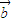 满足|
满足| |=|
|=| |=2,
|=2, •
• =0,若向量向量
=0,若向量向量 与
与 -
- 共线,则|
共线,则|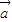 +
+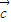 |的最小值为( )
|的最小值为( )A.

B.1
C.
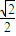
D.

【答案】分析:由已知中向量 ,
, 满足:|
满足:|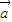 |=|
|=| |=2,
|=2,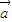 •
• =0,向量
=0,向量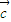 与
与 -
- 共线,我们可得|
共线,我们可得|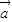 +
+ |=
|= ,进而根据二次函数的性质,得到答案.
,进而根据二次函数的性质,得到答案.
解答:解:∵| |=|
|=|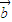 |=2,
|=2, •
• =0,
=0,
又∵向量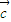 与
与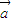 -
- 共线
共线
设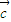 =λ(
=λ( -
-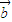 )
)
则|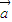 +
+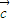 |=|
|=| +λ(
+λ( -
- )|=|(λ+1)
)|=|(λ+1)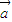 -λ
-λ )|=
)|=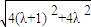 ≥
≥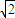
故选A
点评:本题考查的知识点是平面向量数量积的坐标表示、模、夹角,其中根据已知表示出| +
+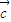 |,将问题转化为求二次函数的最值,是解答本题的关键.
|,将问题转化为求二次函数的最值,是解答本题的关键.
 ,
, 满足:|
满足:|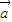 |=|
|=| |=2,
|=2,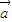 •
• =0,向量
=0,向量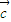 与
与 -
- 共线,我们可得|
共线,我们可得|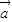 +
+ |=
|= ,进而根据二次函数的性质,得到答案.
,进而根据二次函数的性质,得到答案.解答:解:∵|
 |=|
|=|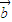 |=2,
|=2, •
• =0,
=0,又∵向量
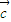 与
与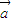 -
- 共线
共线设
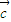 =λ(
=λ( -
-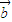 )
)则|
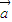 +
+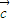 |=|
|=| +λ(
+λ( -
- )|=|(λ+1)
)|=|(λ+1)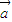 -λ
-λ )|=
)|=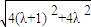 ≥
≥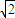
故选A
点评:本题考查的知识点是平面向量数量积的坐标表示、模、夹角,其中根据已知表示出|
 +
+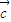 |,将问题转化为求二次函数的最值,是解答本题的关键.
|,将问题转化为求二次函数的最值,是解答本题的关键. 
练习册系列答案
相关题目
 、
、 满足
满足 ,则
,则 .
. ,实数
,实数 满足
满足 ,则
,则 的最小值为( )
的最小值为( ) B.1 C.
B.1 C. D.
D.
 ,
, 满足
满足 ,
, ,
, ,则
,则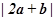 的值为_______.
的值为_______.