题目内容
过双曲线
-
=1(m>0,n>0)上的点P(
,-
)作圆x2+y2=m的切线,切点为A、B,若
•
=0,则该双曲线的离心率的值是( )
| x2 |
| m |
| y2 |
| n |
| 5 |
| 3 |
| PA |
| PB |
分析:如图,根据向量的数量积
•
=0得出∠APB=90°,又PA=PB,PA,PB是圆的切线,从而四边形OAPB是正方形,利用OA=
OP求出m的值,又因为双曲线
-
=1(m>0,n>0)上的点P(
,-
),求出n的值,从而得出该双曲线的离心率的值.
| PA |
| PB |
| ||
| 2 |
| x2 |
| m |
| y2 |
| n |
| 5 |
| 3 |
解答: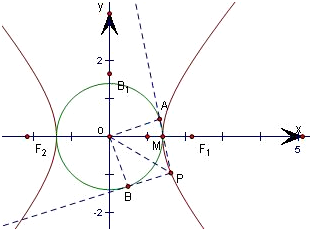 解:如图,∵
解:如图,∵
•
=0,∴
⊥
,
∴∠APB=90°,又PA=PB,PA,PB是圆的切线,
∴四边形OAPB是正方形,
∴OA=
OP=
×2
=2,
即
=2,∴m=4,
又因为双曲线
-
=1(m>0,n>0)上的点P(
,-
),
∴
-
=1,∴n=12,
则该双曲线的离心率的值是
e=
=
=
=2.
故选C.
 解:如图,∵
解:如图,∵| PA |
| PB |
| PA |
| PB |
∴∠APB=90°,又PA=PB,PA,PB是圆的切线,
∴四边形OAPB是正方形,
∴OA=
| ||
| 2 |
| ||
| 2 |
| 2 |
即
| m |
又因为双曲线
| x2 |
| m |
| y2 |
| n |
| 5 |
| 3 |
∴
| 5 |
| m |
| 3 |
| n |
则该双曲线的离心率的值是
e=
| c |
| a |
| ||
| 2 |
| ||
| 2 |
故选C.
点评:本小题主要考查双曲线的简单性质、直线与圆的位置关系、双曲线的标准方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目