题目内容
已知向量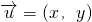 与
与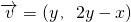 的对应关系用
的对应关系用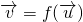 表示.
表示.
(Ⅰ)设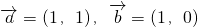 ,求向量
,求向量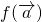 及
及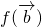 的坐标;
的坐标;
(Ⅱ)求使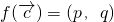 ,(p,q为常数)的向量
,(p,q为常数)的向量 的坐标;
的坐标;
(Ⅲ)证明:对于任意向量 及常数m,n恒有
及常数m,n恒有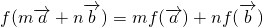 成立.
成立.
解:(I)由已知得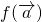 =(1,1),
=(1,1),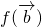 =(0,-1)
=(0,-1)
(II)设 =(x,y),则
=(x,y),则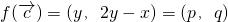 ,
,
∴y=p,x=2p-q,即 =(2P-q,p).
=(2P-q,p).
(III)设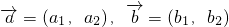 ,则
,则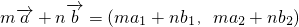 ,
,
故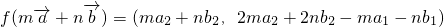 =m(a2,2a2-a1)+n(b2,2b2-b1),
=m(a2,2a2-a1)+n(b2,2b2-b1),
∴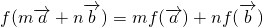
分析:(I)由已知中向量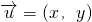 与
与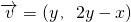 的对应关系用
的对应关系用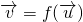 表示,我们根据
表示,我们根据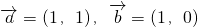 ,易得向量
,易得向量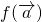 及
及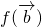 的坐标;
的坐标;
(II)设 =(x,y),根据
=(x,y),根据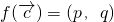 ,我们可以构造关于x,y的方程,解方程即可求出向量
,我们可以构造关于x,y的方程,解方程即可求出向量 的坐标;
的坐标;
(Ⅲ)设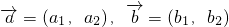 ,分别求出
,分别求出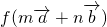 和
和 的坐标,比照后即可得到结论.
的坐标,比照后即可得到结论.
点评:本题考查的知识点是平面向量的坐标运算,其中正确理解新定义向量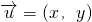 与
与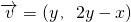 的对应关系用
的对应关系用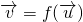 表示是解答本题的关键.
表示是解答本题的关键.
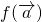 =(1,1),
=(1,1),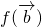 =(0,-1)
=(0,-1)(II)设
 =(x,y),则
=(x,y),则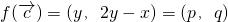 ,
,∴y=p,x=2p-q,即
 =(2P-q,p).
=(2P-q,p).(III)设
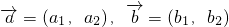 ,则
,则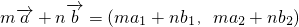 ,
,故
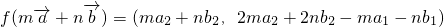 =m(a2,2a2-a1)+n(b2,2b2-b1),
=m(a2,2a2-a1)+n(b2,2b2-b1),∴
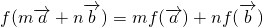
分析:(I)由已知中向量
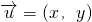 与
与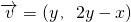 的对应关系用
的对应关系用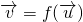 表示,我们根据
表示,我们根据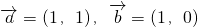 ,易得向量
,易得向量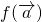 及
及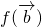 的坐标;
的坐标;(II)设
 =(x,y),根据
=(x,y),根据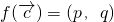 ,我们可以构造关于x,y的方程,解方程即可求出向量
,我们可以构造关于x,y的方程,解方程即可求出向量 的坐标;
的坐标;(Ⅲ)设
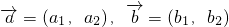 ,分别求出
,分别求出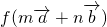 和
和 的坐标,比照后即可得到结论.
的坐标,比照后即可得到结论.点评:本题考查的知识点是平面向量的坐标运算,其中正确理解新定义向量
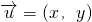 与
与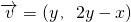 的对应关系用
的对应关系用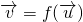 表示是解答本题的关键.
表示是解答本题的关键. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 与向量
与向量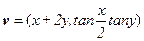 的对应关系可用
的对应关系可用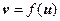 表示.试问是否存在向量
表示.试问是否存在向量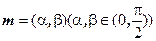 ,使得
,使得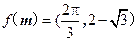 成立?如果存在,求出向量
成立?如果存在,求出向量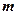 ;如果不存在,请说明理由.
;如果不存在,请说明理由.
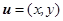 与向量
与向量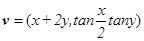 的对应关系可用
的对应关系可用 表示.试问是否存在向量
表示.试问是否存在向量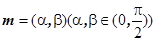 ,使得
,使得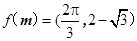 成立?如果存在,求出向量
成立?如果存在,求出向量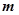 ;如果不存在,请说明理由.
;如果不存在,请说明理由.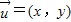 与
与 的对应关系用
的对应关系用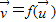 表示.
表示.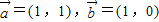 ,求向量
,求向量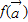 及
及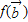 的坐标;
的坐标; ,(p,q为常数)的向量
,(p,q为常数)的向量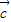 的坐标;
的坐标;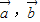 及常数m,n恒有
及常数m,n恒有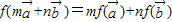 成立.
成立.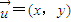 与
与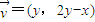 的对应关系用
的对应关系用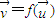 表示.
表示.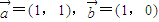 ,求向量
,求向量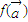 及
及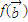 的坐标;
的坐标;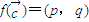 ,(p,q为常数)的向量
,(p,q为常数)的向量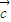 的坐标;
的坐标;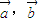 及常数m,n恒有
及常数m,n恒有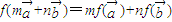 成立.
成立.