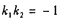题目内容
若在直线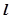 上存在不同的三个点
上存在不同的三个点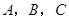 ,使得关于实数
,使得关于实数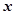 的方程
的方程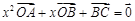 有解(点
有解(点 不在
不在 上),则此方程的解集为( )
上),则此方程的解集为( )
 上存在不同的三个点
上存在不同的三个点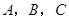 ,使得关于实数
,使得关于实数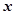 的方程
的方程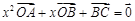 有解(点
有解(点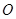 不在
不在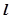 上),则此方程的解集为( )
上),则此方程的解集为( )A. | B.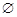 | C.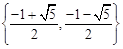 | D.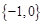 |
A
本题考查三点共线的条件
由向量的减法法则有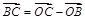 ;
;
又 ,则
,则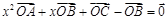 ,即
,即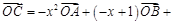
因为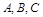 共线于直线
共线于直线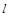 ,所以
,所以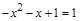 ,即
,即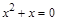 ,解得
,解得 或
或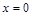 ,
,
当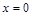 时
时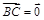 ,即
,即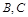 重合,与条件“不同的三个点
重合,与条件“不同的三个点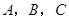 ”矛盾,故有
”矛盾,故有
所以此方程的解集为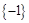
故正确答案为A
注:设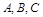 三点共线于直线
三点共线于直线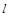 ,
, 为直线外
为直线外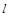 的一点,若
的一点,若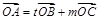 ,则必有
,则必有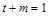
由向量的减法法则有
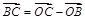 ;
;又
 ,则
,则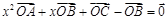 ,即
,即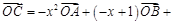
因为
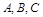 共线于直线
共线于直线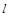 ,所以
,所以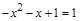 ,即
,即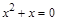 ,解得
,解得 或
或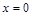 ,
,当
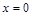 时
时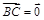 ,即
,即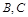 重合,与条件“不同的三个点
重合,与条件“不同的三个点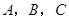 ”矛盾,故有
”矛盾,故有
所以此方程的解集为
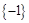
故正确答案为A
注:设
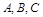 三点共线于直线
三点共线于直线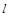 ,
, 为直线外
为直线外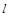 的一点,若
的一点,若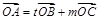 ,则必有
,则必有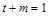

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
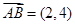 ,
,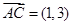 ,则
,则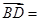 ( )
( )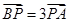 ,
,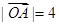 ,
,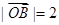 ,且
,且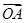 与
与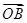 的夹角为60°,则
的夹角为60°,则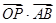 = ▲ .
= ▲ .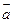 ,
,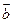 为两个相互垂直的单位向量.已知
为两个相互垂直的单位向量.已知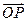 =
=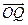 =
=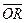 =r
=r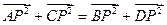 ,则四边形ABCD是( )
,则四边形ABCD是( ) ,
, ,其中
,其中 和
和 不共线,
不共线,  与
与 共线,则
共线,则 .
. =(2,1),
=(2,1), =(1,7),
=(1,7), =(5,1),设X是直线OP上的一点(O为坐标原点),那么
=(5,1),设X是直线OP上的一点(O为坐标原点),那么 的最小值是 ( )
的最小值是 ( )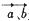 是不共线的向量,若
是不共线的向量,若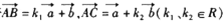 ,则、B、C三点共线的充要条件是
,则、B、C三点共线的充要条件是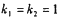 B.
B.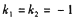 C.
C.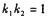 D.
D.