题目内容
(本小题满分12分)口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(1)求甲赢且编号的和为6的事件发生的概率;
(2)这种游戏规则公平吗?试说明理由.
(1)设“甲胜且两数字之和为6”为事件A,事件A包含的基本事件为(1,5),(2,4),(3,3),(4,2),
(5,1),共5个. 又甲、乙二人取出的数字共有5×5=25(个)等可能的结果, 所以P(A)=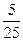 =
=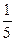 .
.
答:编号的和为6的概率为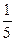 .
.
(2)这种游戏规则不公平.
设“甲胜”为事件B,“乙胜”为事件C,则甲胜即两数字之和为偶数所包含的基本事件数为13个:
(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),(3,3),(3,5),(4,2),(4,4),(5,1),(5,3),(5,1) 所以甲胜的概率P(B)=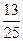 ,从而乙胜的概率P(C)=1-P(B)=1-
,从而乙胜的概率P(C)=1-P(B)=1-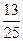 =
=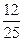 .
.
由于P(B)≠P(C),所以这种游戏规则不公平.
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
编号为 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
| 运动员编号 |  | 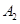 | 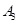 | 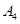 | 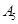 | 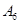 | 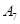 | 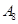 |
| 得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
| 运动员编号 | 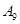 | 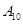 | 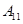 | 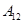 | 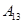 | 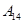 | 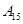 | 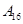 |
| 得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
(Ⅰ)将得分在对应区间内的人数填入相应的空格;
| 区间 |  | 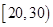 | 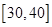 |
| 人数 | | | |
(Ⅱ)从得分在区间
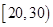 内的运动员中随机抽取2人,
内的运动员中随机抽取2人,(i)用运动员的编号列出所有可能的抽取结果;
(ii)求这2人得分之和大于50的概率.
 个等级,等级系数
个等级,等级系数 依次为
依次为 ,其中
,其中 为标准
为标准 ,
, 为标准
为标准 ,产品的等级系数越大表明产品的质量越好,已知某厂执行标准
,产品的等级系数越大表明产品的质量越好,已知某厂执行标准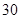 件,相应的等级系数组成一个样本,数据如下:
件,相应的等级系数组成一个样本,数据如下: 的为一等品,等级系数
的为一等品,等级系数 的为二等品,等级系数
的为二等品,等级系数 的为三等品.
的为三等品.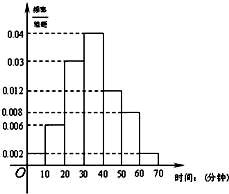
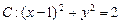 ,点
,点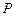 是圆内的任意一点,直线
是圆内的任意一点,直线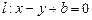 .
.  ;
;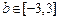 ,求直线
,求直线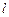 与
与 圆
圆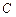 相交的概率.
相交的概率.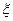 ,求随机变量
,求随机变量