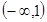题目内容
当 时,
时, 恒成立,则实数a的取值范围是 .
恒成立,则实数a的取值范围是 .
【答案】分析:由题意当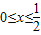 时,
时,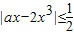 恒成立,可得-
恒成立,可得- ≤ax-2x3≤
≤ax-2x3≤ ,化为两个恒成立问题,从而求解.
,化为两个恒成立问题,从而求解.
解答:解:∵当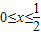 时,
时,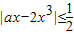 恒成立,
恒成立,
∴- ≤ax-2x3≤
≤ax-2x3≤ ,
,
∴ax-2x3+ ≥0和ax-2x3-
≥0和ax-2x3- ≤0,在[0,
≤0,在[0, ]上恒成立;
]上恒成立;
∴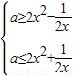 ,下求出2x2-
,下求出2x2-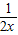 的最大值和2x2+
的最大值和2x2+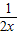 的最小值,
的最小值,
∵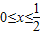 ,∵2x2-
,∵2x2-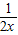 在
在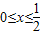 上增函数,∴2x2-
上增函数,∴2x2-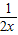 ≤2×
≤2× -1=-
-1=- ,
,
∴a≥- ;
;
∵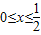 ,∵2x2+
,∵2x2+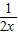 ≥2×
≥2× +1=
+1= ,∴a≤
,∴a≤ ,
,
∴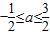 ,
,
故答案为: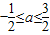 .
.
点评:此题考查绝对值不等式的性质及函数的恒成立问题,这类题目是高考的热点,难度不是很大,要注意函数的增减性.
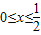 时,
时,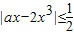 恒成立,可得-
恒成立,可得- ≤ax-2x3≤
≤ax-2x3≤ ,化为两个恒成立问题,从而求解.
,化为两个恒成立问题,从而求解.解答:解:∵当
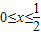 时,
时,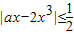 恒成立,
恒成立,∴-
 ≤ax-2x3≤
≤ax-2x3≤ ,
,∴ax-2x3+
 ≥0和ax-2x3-
≥0和ax-2x3- ≤0,在[0,
≤0,在[0, ]上恒成立;
]上恒成立;∴
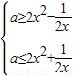 ,下求出2x2-
,下求出2x2-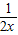 的最大值和2x2+
的最大值和2x2+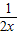 的最小值,
的最小值,∵
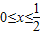 ,∵2x2-
,∵2x2-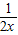 在
在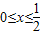 上增函数,∴2x2-
上增函数,∴2x2-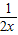 ≤2×
≤2× -1=-
-1=- ,
,∴a≥-
 ;
;∵
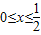 ,∵2x2+
,∵2x2+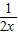 ≥2×
≥2× +1=
+1= ,∴a≤
,∴a≤ ,
,∴
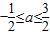 ,
,故答案为:
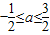 .
.点评:此题考查绝对值不等式的性质及函数的恒成立问题,这类题目是高考的热点,难度不是很大,要注意函数的增减性.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
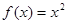 ,,若存在实数
,,若存在实数 ,当
,当 时,
时,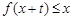 恒成立,则实数
恒成立,则实数 的最大值为 .
的最大值为 . D.
D.
 ,若当
,若当 时,
时, 恒成立,
恒成立, 的取值范围是( )
的取值范围是( ) ) B.
(-1,+
) B.
(-1,+ 时,
时, 恒成立,则实数
恒成立,则实数 的取值范围是___________.
的取值范围是___________.

 ,当
,当 时,
时, 恒成立,则实数
恒成立,则实数 的取值范围是【 】
的取值范围是【 】 B.
B. C.
C.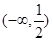 D.
D.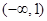
 ,当
,当 时,
时, 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( ) B.
B. C .
C . D .
D .