题目内容
已知双曲线 的右顶点为A(2,0),一条渐近线为
的右顶点为A(2,0),一条渐近线为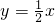 ,过点B(0,2)且斜率为k的直线l与该双曲线交于不同的两点P,Q.
,过点B(0,2)且斜率为k的直线l与该双曲线交于不同的两点P,Q.
(I)求双曲线的方程及k的取值范围;
(II)是否存在常数k,使得向量 垂直?如果存在,求k的值;如果不存在,请说明理由.
垂直?如果存在,求k的值;如果不存在,请说明理由.
解:(I)由题意,a=2,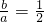 ,∴b=1
,∴b=1
∴双曲线的方程为
设直线l的方程为y=kx+2,代入双曲线方程,可得(4k2-1)x2+16kx+20=0
∵过点B(0,2)且斜率为k的直线l与该双曲线交于不同的两点P,Q
∴4k2-1≠0且△=256k2-80(4k2-1)>0,即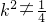 且
且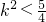
解得- <k<
<k< 且k≠
且k≠ ;
;
(II)设P(x1,y1),Q(x2,y2),则x1+x2=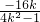 ,
,
∵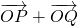 =(x1+x2,y1+y2),
=(x1+x2,y1+y2), =(-2,2),
=(-2,2),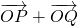 与
与 垂直
垂直
∴-2(x1+x2)+2(y1+y2)=0
∴(x1+x2)(k-1)+4=0
∴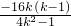 +4=0
+4=0
∴k=
∴存在常数k= ,使得向量
,使得向量 垂直.
垂直.
分析:(I)由题意,a=2,一条渐近线为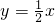 ,可得b的值,从而可得双曲线的方程;设出直线方程代入双曲线方程,利用根的判别式,即可求k的取值范围;
,可得b的值,从而可得双曲线的方程;设出直线方程代入双曲线方程,利用根的判别式,即可求k的取值范围;
(II)用坐标表示向量,利用向量的数量积为0,建立方程,即可得到结论.
点评:本题考查双曲线的标准方程,考查直线与双曲线的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.
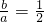 ,∴b=1
,∴b=1∴双曲线的方程为

设直线l的方程为y=kx+2,代入双曲线方程,可得(4k2-1)x2+16kx+20=0
∵过点B(0,2)且斜率为k的直线l与该双曲线交于不同的两点P,Q
∴4k2-1≠0且△=256k2-80(4k2-1)>0,即
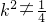 且
且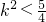
解得-
 <k<
<k< 且k≠
且k≠ ;
;(II)设P(x1,y1),Q(x2,y2),则x1+x2=
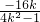 ,
,∵
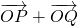 =(x1+x2,y1+y2),
=(x1+x2,y1+y2), =(-2,2),
=(-2,2),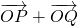 与
与 垂直
垂直∴-2(x1+x2)+2(y1+y2)=0
∴(x1+x2)(k-1)+4=0
∴
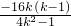 +4=0
+4=0∴k=

∴存在常数k=
 ,使得向量
,使得向量 垂直.
垂直.分析:(I)由题意,a=2,一条渐近线为
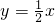 ,可得b的值,从而可得双曲线的方程;设出直线方程代入双曲线方程,利用根的判别式,即可求k的取值范围;
,可得b的值,从而可得双曲线的方程;设出直线方程代入双曲线方程,利用根的判别式,即可求k的取值范围;(II)用坐标表示向量,利用向量的数量积为0,建立方程,即可得到结论.
点评:本题考查双曲线的标准方程,考查直线与双曲线的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 的右顶点为A,右焦点为F,右准线与
的右顶点为A,右焦点为F,右准线与 轴交于点B,且与一条渐近线交于点C,点O为坐标原点,
轴交于点B,且与一条渐近线交于点C,点O为坐标原点, ,
, ,过点F的直线
,过点F的直线 与双曲线右支交于点
与双曲线右支交于点 .
. 面积的最小值.
面积的最小值. 的右顶点为A,右焦点为F,右准线与
的右顶点为A,右焦点为F,右准线与 轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又
轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又 ,
, 过点F的直线与双曲线右交于点M、N,点P为点M关于
过点F的直线与双曲线右交于点M、N,点P为点M关于 面积的最小值。
面积的最小值。 的右顶点为E,过双曲线的左焦点且垂直于
的右顶点为E,过双曲线的左焦点且垂直于 轴的直线与该双曲线相交A、B两点,若
轴的直线与该双曲线相交A、B两点,若 ,则该双曲线的离心率
,则该双曲线的离心率 是( )
是( ) B.2 C.
B.2 C. D.不存在
D.不存在