题目内容
数列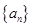 满足
满足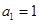 ,
,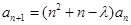 (
(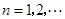 ),
),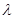 是常数.
是常数.
(Ⅰ)当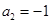 时,求
时,求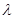 及
及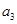 的值;
的值;
(Ⅱ)数列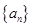 是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由.
是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由.
【答案】
(Ⅰ) .
. .
.
(Ⅱ)对任意 ,数列
,数列 都不可能是等差数列.
都不可能是等差数列.
【解析】
试题分析:(Ⅰ)由于 ,且
,且 .
.
所以当 时,得
时,得 ,故
,故 .
.
从而 .
6分
.
6分
(Ⅱ)数列 不可能为等差数列,证明如下:
不可能为等差数列,证明如下:
由 ,
, 得
得
 ,
, ,
, .
.
若存在 ,使
,使 为等差数列,则
为等差数列,则 ,
,
即 ,解得
,解得 .
.
于是 ,
, .
.
这与 为等差数列矛盾.所以,对任意
为等差数列矛盾.所以,对任意 ,数列
,数列 都不可能是等差数列.
12分
都不可能是等差数列.
12分
考点:本题主要考查数列的递推公式,等差数列的定义,反证法。
点评:中档题,本题综合性较强,特别是(2)探究数列的特征,利用反证法证明数列不可能是等差数列。注意,首先假设某命题不成立(即在原命题的条件下,结论不成立),然后推理出明显矛盾的结果,从而下结论说原假设不成立,原命题得证。一定要用到“反设”,法则表示反证法。

练习册系列答案
相关题目