题目内容
当0<k<
时,方程
=kx的解的个数是( )
| 1 |
| 2 |
| |1-x| |
| A、0 | B、1 | C、2 | D、3 |
分析:此题关键在于分类讨论,注意x>0的前提,讨论x的值,去绝对值,根据判别式进行判定根的个数.
解答:解:方程两边平方|1-x|=(kx)2,并且由原方程还得出x>0
①x=1,左边=0,右边由于k≠0所以不为零.所以x=1不是解.
②x>1,去绝对值符号:x-1=k2x2即k2x2-x+1=0
判别式△=1-4k2由于0<k<
,故△∈(0,1)所以有两个解.
当然还需要判断这两个解是不是都大于1的.的确,这是显然的,因为方程x-1=k2x2右边一定大于0,故两解一定是大于1的.
③x<1,去绝对值符号:1-x=k2x2即k2x2+x-1=0判别式△=1+4k2>0所以有两个解.
同样,因为方程1-x=k2x2右边一定大于0,故两解一定是小于1的.但是,还需要判断这两个解是否都大于零.
由根与系数的关系:两根之积:-
<0这就说明两根一正一负!那个负根是不能要的,所以舍去总共3个解
故选D.
①x=1,左边=0,右边由于k≠0所以不为零.所以x=1不是解.
②x>1,去绝对值符号:x-1=k2x2即k2x2-x+1=0
判别式△=1-4k2由于0<k<
| 1 |
| 2 |
当然还需要判断这两个解是不是都大于1的.的确,这是显然的,因为方程x-1=k2x2右边一定大于0,故两解一定是大于1的.
③x<1,去绝对值符号:1-x=k2x2即k2x2+x-1=0判别式△=1+4k2>0所以有两个解.
同样,因为方程1-x=k2x2右边一定大于0,故两解一定是小于1的.但是,还需要判断这两个解是否都大于零.
由根与系数的关系:两根之积:-
| 1 |
| k2 |
故选D.
点评:本题主要考查了函数与方程的综合运用,以及分类讨论的思想,解题时需注意前提条件,需要细心研究,属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
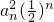 的前n项和.
的前n项和. 的前n项和.
的前n项和.