题目内容
如图,F1,F2分别是椭圆 (a>b>0)的左、右焦点,M为椭圆上一点,MF2垂直于x轴,椭圆下顶点和右顶点分别为A、B,且OM∥AB,
(a>b>0)的左、右焦点,M为椭圆上一点,MF2垂直于x轴,椭圆下顶点和右顶点分别为A、B,且OM∥AB,
(1)求椭圆的离心率;
(2)过F2作于OM垂直的直线交椭圆于点P、Q,若 ,求椭圆的方程。
,求椭圆的方程。
 (a>b>0)的左、右焦点,M为椭圆上一点,MF2垂直于x轴,椭圆下顶点和右顶点分别为A、B,且OM∥AB,
(a>b>0)的左、右焦点,M为椭圆上一点,MF2垂直于x轴,椭圆下顶点和右顶点分别为A、B,且OM∥AB,(1)求椭圆的离心率;
(2)过F2作于OM垂直的直线交椭圆于点P、Q,若
 ,求椭圆的方程。
,求椭圆的方程。 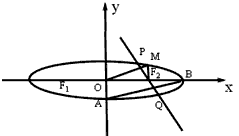
解:(1)设F1(-c,0),F2(c,0),则M(c,y),
∴A(0,-b),B(a,0),且OM∥AB, ∴kOM=kAB,
∴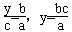 ,
,
又点M在椭圆上,
∴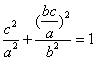 ,∴e=
,∴e=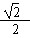 ;
;
(2)由(1)得a=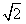 c,b=c,
c,b=c,
∴椭圆的方程为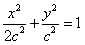 ,
,
∵kAB=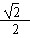 ,
,
∴直线PQ的方程为y=-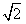 (x-c),
(x-c),
∴点F1到直线PQ的距离d=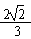 c,
c,
又由 ,
,
设P(x1,y1),Q(x2,y2),
∴x1+x2=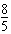 c, x1x2=
c, x1x2= ,
,
∴|PQ|=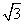 |x1-x2|=
|x1-x2|=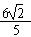 c,
c,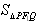 =
=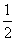 +
+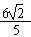 c·
c·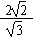 c=20,
c=20,
∴c2=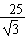 ,
,
∴a2=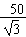 ,b2=
,b2= ,
,
∴椭圆的方程为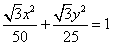 。
。

练习册系列答案
相关题目
 如图,F1,F2分别为椭圆
如图,F1,F2分别为椭圆 如图,F1、F2分别为椭圆
如图,F1、F2分别为椭圆 如图,F1,F2分别为双曲线
如图,F1,F2分别为双曲线 如图,F1、F2分别为椭圆
如图,F1、F2分别为椭圆 的左、右焦点,点P在椭圆上,△POF2是面积
的左、右焦点,点P在椭圆上,△POF2是面积 的正三角形,则
的正三角形,则 的值是
的值是