题目内容
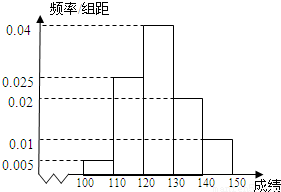
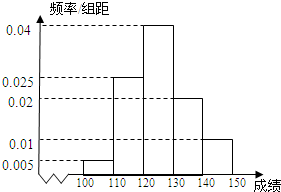 长春市某中学高三(1)班40名学生在一次数学测验中,成绩全部介于100分与150分之间,将测验成绩按如下方式分成五组:第一组[100,110);第二组[110,120),…,第五组[140,150].右图是按上述分组方法得到的频率分布直方图.
长春市某中学高三(1)班40名学生在一次数学测验中,成绩全部介于100分与150分之间,将测验成绩按如下方式分成五组:第一组[100,110);第二组[110,120),…,第五组[140,150].右图是按上述分组方法得到的频率分布直方图.
(I)若成绩在130分以上为优秀,求该班在这次测验中成绩优秀的人数;
(II)估计该班在这次测验中的平均分(同一组中的数据用该组区间的中点值作代表);
(III)该班有3名学生因故未参加考试,如果他们参加考试,且彼此之间的成绩不受影响,以已知样本数据的频率作为这3名同学成绩的概率.试求这3名学生中至少有1人成绩不低于130分的概率.
解:(I)由直方图知,成绩在[130,150]内的人数为:40×0.2+40×0.1=12 (人)
所以该班成绩优秀的人数为12人.
(II)设该班在这次测验中的平均分为 ,
,
则 =105×0.05+115×0.25+125×0.4+135×0.2+145×0.1=125.5(分).
=105×0.05+115×0.25+125×0.4+135×0.2+145×0.1=125.5(分).
(III)每1名学生成绩不低于130的概率为 p=0.2+0.1=0.3.
设这3名学生中至少有1人成绩不低于130分为事件A,其对立事件为:这3名学生成绩全部低于130分,
P(A)=1-C30×0.73=1-0.343=0.657.
分析:(I)由直方图知,成绩在[130,150]内的人数为:40×0.2+40×0.1,运算求得结果.
(II)设该班在这次测验中的平均分为 ,则
,则 =105×0.05+115×0.25+125×0.4+135×0.2+145×0.1,运算求得结果.
=105×0.05+115×0.25+125×0.4+135×0.2+145×0.1,运算求得结果.
(III)每1名学生成绩不低于130的概率为 p=0.3,这3名学生中至少有1人成绩不低于130分的概率为1-C30×0.73=,
运算求得结果.
点评:本题考查n次独立重复实验中恰好发生k次的概率,等可能事件的概率,所求的事件与它的对立事件概率间的关系,
得到每1名学生成绩不低于130的概率为 p=0.3,是解题的关键.
所以该班成绩优秀的人数为12人.
(II)设该班在这次测验中的平均分为
 ,
,则
 =105×0.05+115×0.25+125×0.4+135×0.2+145×0.1=125.5(分).
=105×0.05+115×0.25+125×0.4+135×0.2+145×0.1=125.5(分).(III)每1名学生成绩不低于130的概率为 p=0.2+0.1=0.3.
设这3名学生中至少有1人成绩不低于130分为事件A,其对立事件为:这3名学生成绩全部低于130分,
P(A)=1-C30×0.73=1-0.343=0.657.
分析:(I)由直方图知,成绩在[130,150]内的人数为:40×0.2+40×0.1,运算求得结果.
(II)设该班在这次测验中的平均分为
 ,则
,则 =105×0.05+115×0.25+125×0.4+135×0.2+145×0.1,运算求得结果.
=105×0.05+115×0.25+125×0.4+135×0.2+145×0.1,运算求得结果.(III)每1名学生成绩不低于130的概率为 p=0.3,这3名学生中至少有1人成绩不低于130分的概率为1-C30×0.73=,
运算求得结果.
点评:本题考查n次独立重复实验中恰好发生k次的概率,等可能事件的概率,所求的事件与它的对立事件概率间的关系,
得到每1名学生成绩不低于130的概率为 p=0.3,是解题的关键.

练习册系列答案
相关题目
 长春市某中学高三(1)班40名学生在一次数学测验中,成绩全部介于100分与150分之间,将测验成绩按如下方式分成五组:第一组[100,110);第二组[110,120),…,第五组[140,150].右图是按上述分组方法得到的频率分布直方图.
长春市某中学高三(1)班40名学生在一次数学测验中,成绩全部介于100分与150分之间,将测验成绩按如下方式分成五组:第一组[100,110);第二组[110,120),…,第五组[140,150].右图是按上述分组方法得到的频率分布直方图.