题目内容
已知△ABC的内角A、B、C所对的边分别为a,b,c,且a=2, cosB= .
.
(1)若b=4,求sinA的值; (2) 若△ABC的面积S△ABC=4,求b,c的值.
(1) 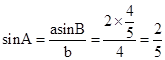 .
.
(2)  .
.
解析试题分析:(1) ∵cosB= >0,且0<B<π,
>0,且0<B<π,
∴sinB=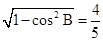 .
.
由正弦定理得 ,
,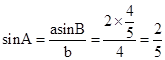 .
.
(2) ∵S△ABC=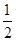 acsinB=4,
acsinB=4,
∴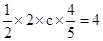 , ∴c="5."
, ∴c="5."
由余弦定理得b2=a2+c2-2accosB,
∴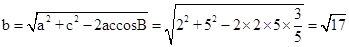 .
.
考点:本题主要考查三角函数同角公式,正弦定理、余弦定理的应用。
点评:中档题,本题综合考查三角函数同角公式,正弦定理、余弦定理的应用。应用同角公式的“平方关系”解题时,要注意角的范围,以正确确定函数值的正负。本题解答思路明确,难度不大。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 分别是角A,B,C的对边,
分别是角A,B,C的对边, ,
,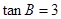 .
.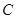 的值;
的值; ,求△ABC面积.
,求△ABC面积. 中,角
中,角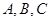 的对边分别为
的对边分别为 .
.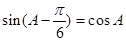 ,求角
,求角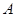 的大小;
的大小;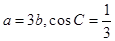 ,求
,求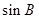 的值.
的值. 中,
中, 分别是角
分别是角 的对边,若
的对边,若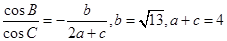 ,求△
,求△ 中,
中,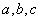 分别是角
分别是角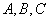 的对边,
的对边, ,
, ,且
,且
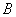 的大小;
的大小; 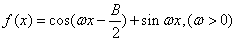 ,且
,且 的最小正周期为
的最小正周期为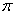 ,求
,求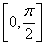 上的最大值和最小值,及相应的
上的最大值和最小值,及相应的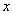 的值。
的值。 处,发现北偏东
处,发现北偏东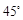 方向,距
方向,距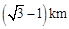 的
的 处有一艘走私船,在
处有一艘走私船,在 方向,距
方向,距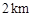 的
的 处的缉私船奉命以
处的缉私船奉命以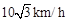 的速度追截走私船,此时走私船正以
的速度追截走私船,此时走私船正以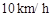 的速度从
的速度从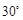 方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间. (
方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间. (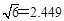 )
)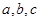 分别为
分别为 三个内角
三个内角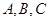 的对边,
的对边,
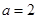 ,
,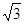 ;求
;求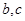 .
. ABC中,
ABC中, 所对边分别为
所对边分别为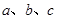 ,且满足
,且满足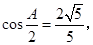
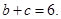
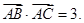
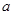 的值;
的值;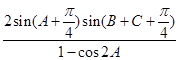 的值.
的值.  是函数
是函数 图象上的任意两点,若
图象上的任意两点,若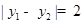 时,
时, 的最小值为
的最小值为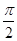 ,且函数
,且函数 的图像经过点
的图像经过点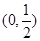 .
. 中,角
中,角 的对边分别为
的对边分别为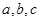 ,且
,且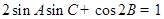 ,求
,求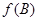 的取值范围.
的取值范围.