题目内容
(本题满分13分)如图,在四棱锥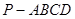 中,底面
中,底面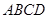 是矩形,知
是矩形,知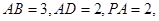
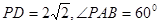 。
。

(1)证明: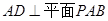 ;
;
(2)求异面直线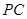 与
与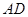 所成的角的余弦值;
所成的角的余弦值;
(3)求二面角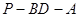 的大小余弦值。
的大小余弦值。
【答案】
(1) ,
, ,
,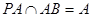
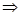
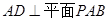 ;(2)
;(2) ;(3)
;(3)
【解析】
试题分析:(1)证明:在 中,由题设
中,由题设 ,
,
可得 ,于是
,于是 ,
,
在矩形 中,
中, ,
,
又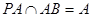 ,所以
,所以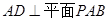 ; ……4分
; ……4分
(2)由题意得,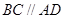 ,
,
所以 (或其补角)是异面直线
(或其补角)是异面直线 与
与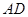 所成的角在
所成的角在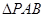 中,
中,
由余弦定理得 ,
,
由(1)知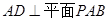 ,
, ,
,
所以 ,因而
,因而 ,
,
故 是直角三角形,
是直角三角形,
所以 ,
,
所以异面直线 与
与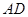 所成的角的余弦值为
所成的角的余弦值为 ; ……9分
; ……9分
(3)过点 做
做 于
于 ,过点
,过点 做
做 于
于 ,连接
,连接
因为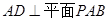 ,
, ,
, ,又
,又 ,
,
所以 ,
,
故 为
为 在平面
在平面 内的射影,所以
内的射影,所以 ,
,
故 是二面角
是二面角 的平面角。
的平面角。
由题设可得, ,
,
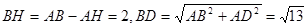 ,
,
于是在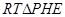 中,
中, ,
,
所以二面角 的余弦值为
的余弦值为 . ……13分
. ……13分
考点:本小题主要考查空间中线面垂直的证明和异面直线所成的角以及二面角的求法,考查学生的空间向量能力、推理论证能力和运算求解能力.
点评:证明直线、平面之间的位置关系时,要注意摆清楚条件,各条件缺一不可,求两条异面直线所成的角时,要注意角的取值范围.

练习册系列答案
相关题目
 在城
在城 的南偏西
的南偏西 的方向上,由
的方向上,由 ,在
,在 处,有一人正沿公路向
处,有一人正沿公路向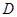 处,此时
处,此时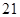 公里,问此人还需要走多少公里到达
公里,问此人还需要走多少公里到达
 中,
中,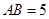 ,
, ,
, ,
, ,
, ,
, 是
是 的中点,设
的中点,设 ,
, ,
, .
.
 表示
表示 ;
; 的长.
的长.
 ,
, ,底面
,底面 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD,  ,O为AD中点.
,O为AD中点.
 与平面
与平面 所成角的余弦值;
所成角的余弦值; 点到平面
点到平面 的距离
的距离 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 中,已知
中,已知
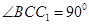 ,
,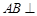 侧面
侧面

 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).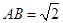 ,求二面角
,求二面角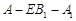 的大小.
的大小.