Question

设f（x）=2sin(4x-

π

3

)
（1）将函数y=f（x）的图象向左平移

π

8

个单位后，再将得到的图象上各点的横坐标伸长到原来的2倍，纵坐标不变，得到函数y=g（x）的图象，求g（x）．并用“五点法”画出y=g（x），x∈[0，π]的图象．
（2）若关于x的方程g（x）=k+1在[0，

π

2

]内有两个不同根α、β，求α+β的值及k的取值范围．

x

Answer 1

分析：（1）根据图象变换规律，可得结论，从而可得函数的图象；
（2）可在同一坐标系中画出函数y=sin（2x+

π

6

）及y=

k+1

2

的图象，借助于图象的直观性求解．

解答：解：（1）由题意，y=2sin（2x+

π

6

）

x	- π 12	π 6	5π 12	2π 3	11π 12
2x+ π 6	0	π 2	π	3π 2	2π
y=2sin（2x+ π 6 ）	0	2	0	-2	0

函数图象如图所示，

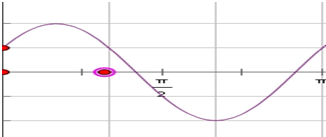
（2）可在同一坐标系中画出函数y=sin（2x+

π

6

）及y=

k+1

2

的图象，借助于图象的直观性求解．
设C：y=sin，l：y=

k+1

2

，在同一坐标系中作出它们的图象如下图．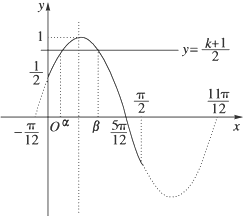
由图易见当

1

2

≤

k+1

2

＜1时，即0≤k＜1时，直线l与曲线C有两个交点，且两交点的横坐标为α、β，从图象中还可看出α、β关于x=

π

3

对称，故α+β=

2π

3

．
综上可知，0≤k＜1，且α+β=

2π

3

．

点评：本题考查三角函数的图象与性质，考查三角函数的图象变换，属于中档题．