题目内容
学校科技小组在计算机上模拟航天器变轨返回试验.设计方案如图244所示:航天器运行(按顺时针方向)的轨迹方程为![]() =1,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、M(0,
=1,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、M(0,![]() )为顶点的抛物线的实线部分,降落点为D(8,0).观测点A(4,0)、B(6,0)同时跟踪航天器.
)为顶点的抛物线的实线部分,降落点为D(8,0).观测点A(4,0)、B(6,0)同时跟踪航天器.
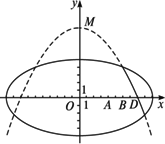
(1)求航天器变轨后的运行轨迹所在的曲线方程;
(2)试问:当航天器在x轴上方时,观测点A、B测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
答案:
解析:
解析:
|
解:(1)设曲线方程为y=ax2+ 由题意可知0=a·64+ ∴曲线方程为y= (2)设变轨点为C(x,y),根据题意可知 得4y2-7y-36=0,y=4或y= ∴y=4得x=6或x=-6(不合题意,舍去). ∴C点的坐标为(6,4),AC= 答:当观测点A、B测得AC、BC距离分别为 思路解析:本题是有关椭圆与双曲线的实际应用问题,所求的抛物线方程不是标准方程的形式,可以将其视为对应的标准方程的抛物线进行了一定的平移后所得到的,从而将问题解决;有关求曲线的交点问题通常是解它们的方程所组成的方程组,从而求解. |

练习册系列答案
相关题目
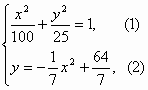
 学校科技小组在计算机上模拟航天器变轨返回试验.设计方案如图:航天器运行(按顺时针方向)的轨迹方程为
学校科技小组在计算机上模拟航天器变轨返回试验.设计方案如图:航天器运行(按顺时针方向)的轨迹方程为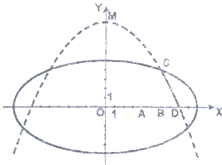 (2006•蚌埠二模)“神六”上天并顺利返回,让越来越多的青少年对航天技术发生了兴趣.某学校科技小组在计算机上模拟航天器变轨返回试验,设计方案
(2006•蚌埠二模)“神六”上天并顺利返回,让越来越多的青少年对航天技术发生了兴趣.某学校科技小组在计算机上模拟航天器变轨返回试验,设计方案
 学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图:航天器运行(按顺时针方向)的轨迹方程为
学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图:航天器运行(按顺时针方向)的轨迹方程为