题目内容
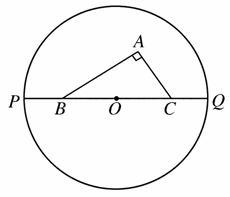
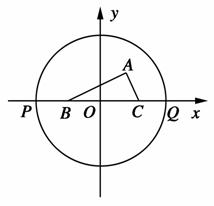
 如图,直角△ABC的顶点A、B分别在x轴、y轴的正半轴上移动,直角顶点C与原点O在直线AB的两侧,则顶点C的轨迹是 ( )
如图,直角△ABC的顶点A、B分别在x轴、y轴的正半轴上移动,直角顶点C与原点O在直线AB的两侧,则顶点C的轨迹是 ( )分析:由题意C在以AB为直径的圆上,由于A、B分别在x轴、y轴的正半轴上移动时,顶点C的轨迹是线段.
解答:解:由题意,设C(x,y),A(a,0),B(0,b),则可知(x-
)2+(y-
)2=
,其中a2+b2=AB2,
所以A、B分别在x轴、y轴的正半轴上移动时,顶点C的轨迹是线段,
故选D.
| a |
| 2 |
| b |
| 2 |
| a2+b2 |
| 4 |
所以A、B分别在x轴、y轴的正半轴上移动时,顶点C的轨迹是线段,
故选D.
点评:本题主要考查曲线轨迹的求法,轨迹是似是而非的圆,因为这个“圆”的圆心[AB的中点]是在“以坐标原点O为圆心,c/2为半径的圆”的四分之一圆弧上滑动的. 需要注意的是“线段”的概念:线段不等于“直线”,也不等于“直线段”[其长度等于两端点之间的距离],而是任意的相连成串的点的轨迹,也就是说,我们在纸上任意画一条或直或弯的线条都叫线段.弄清楚这一点才能真正理解正确答案.

练习册系列答案
相关题目
 如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-
如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-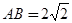 ,
, 为斜边AB的中点,若
为斜边AB的中点,若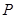 为线段
为线段 上的动点,则
上的动点,则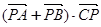 的最大值是
( )
的最大值是
( ) 
 C.
C. 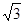 D.
D.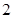
 如图,直角△ABC的顶点A、B分别在x轴、y轴的正半轴上移动,直角顶点C与原点O在直线AB的两侧,则顶点C的轨迹是
如图,直角△ABC的顶点A、B分别在x轴、y轴的正半轴上移动,直角顶点C与原点O在直线AB的两侧,则顶点C的轨迹是