题目内容
如图，三条直线两两平行且不共面，每两条确定一个平面，一共可以确定几个平面？如果三条直线相交于一点，它们最多可以确定几个平面？分析：这三条直线象三棱柱的三条侧棱，根据平面的基本性质可以确定3个平面，得到结果；满足相交于一点的三条直线能够确定一个平面或三个平面，从而得出其最多可以确定几个平面．
解答：解：①三条直线两两平行，这三条直线象三棱柱的三条侧棱，
其中每两条直线可以确定一个平面，则可以确定3个平面；
②∵三条直线两两相交，每两条确定一个平面，
当这三条直线在同一个平面时，则可以确定1个平面；
当这三条直线不在同一个平面时，则可以确定3个平面；
∴这三条直线能够确定一个平面或三个平面，最多可以确定3个平面．
其中每两条直线可以确定一个平面，则可以确定3个平面；
②∵三条直线两两相交，每两条确定一个平面，
当这三条直线在同一个平面时，则可以确定1个平面；
当这三条直线不在同一个平面时，则可以确定3个平面；
∴这三条直线能够确定一个平面或三个平面，最多可以确定3个平面．
点评：本题考查查平面的基本性质及其应用，考查进行简单的合情推理，本题是一个推论应用问题，是一个基础题．
练习册系列答案
快乐5加2金卷系列答案
相关题目
LMN，如果用S1，S2，S3表示三个侧面面积，S4表示截面面积，那么你类比得到的结论是 ．
设想正方形换成正方体，把截线换成如图的截面，这时从正方体上截下三条侧棱两两垂直的三棱锥O—LMN，如果用
表示三个侧面面积，
表示截面面积，那么你类比得到的结论是（ ）
B．
D．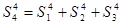
.设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥
,若用
表示三个侧面面积,
表示截面面积,你类比得到的结论是
. 
表示三个侧面面积，
表示截面面积，那么你类比得到的结论是
表示三个侧面面积，
表示截面面积，那么你类比得到的结论是
。