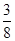题目内容
一个袋中装有大小相同的5个白球和3个红球,现在不放回的取2次球,每次取出一个球,记“第1次拿出的是白球”为事件 ,“第2次拿出的是白球”为事件
,“第2次拿出的是白球”为事件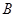 ,则事件
,则事件 与
与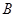 同时发生的概率是( )
同时发生的概率是( )
A.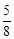 | B.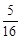 | C.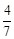 | D.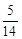 |
D
解析试题分析:从装有大小相同的5个白球和3个红球共8个球的袋中先后不放回的各取出一个球的方法共有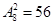 种,事件
种,事件 与
与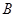 同时发生的即两次中第1次取出的是白球,第2次取出的还是白球,这样的取法有
同时发生的即两次中第1次取出的是白球,第2次取出的还是白球,这样的取法有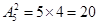 种,由古典概型的概率计算公式得事件
种,由古典概型的概率计算公式得事件 与
与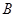 同时发生的概率是
同时发生的概率是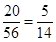 ,故选择D.
,故选择D.
考点:古典概型的概率计算.

练习册系列答案
相关题目
随机变量 的概率分布列规律为
的概率分布列规律为 其中
其中 为常数,则
为常数,则 的值为 ( ).
的值为 ( ).
A. | B. | C. | D. |
设随机变量ξ~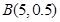 ,又η=5ξ,则Eη和Dη的值分别是( )
,又η=5ξ,则Eη和Dη的值分别是( )
A.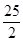 和 和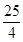 | B.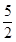 和 和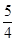 | C.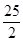 和 和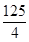 | D.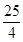 和 和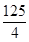 |
 B.
B.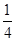 C.
C. D.
D.

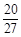
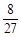

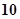 环、
环、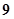 环、
环、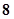 环的概率分别是
环的概率分别是 ,则这位射手在一次射击中不够
,则这位射手在一次射击中不够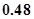
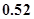
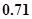
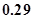
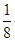 B.
B.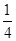 C.
C.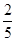 D .
D .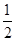
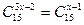 ,求
,求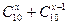 的值;
的值;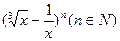 的展开式中第3项为常数项,求
的展开式中第3项为常数项,求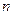 .
.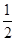 B.
B.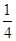 C.
C.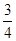 D.
D.