题目内容
已知函数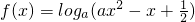 在[1,2]上恒正,则实数a的取值范围是
在[1,2]上恒正,则实数a的取值范围是
- A.
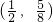
- B.
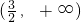
- C.
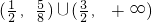
- D.
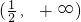
C
分析:设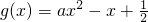 ,由g(x)>0,可得a>
,由g(x)>0,可得a> ,故a>
,故a> ,g(x)在[1,2]上是递增函数.当a>1时,f(x)在[1,2]上是增函数,根据f(1)>0求出a的取值范围;当
,g(x)在[1,2]上是递增函数.当a>1时,f(x)在[1,2]上是增函数,根据f(1)>0求出a的取值范围;当 <a<1时,f(x)在[1,2]上是减函数,由f(2)>0求出a的取值范围,最后把这两个范围取并集.
<a<1时,f(x)在[1,2]上是减函数,由f(2)>0求出a的取值范围,最后把这两个范围取并集.
解答:设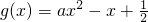 ,由
,由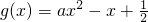 >0,可得 a>
>0,可得 a> .
.
当1≤x≤2时, 的最大值为
的最大值为 ,从而a>
,从而a> .
.
在a> 的前提下,易知函数g(x)的对称轴x=
的前提下,易知函数g(x)的对称轴x= 在区间[1,2]的左边,
在区间[1,2]的左边,
从而g(x)在[1,2]上是递增函数.
当a>1时,f(x)在[1,2]上是增函数,有f(1)=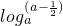 >0=loga1,∴a>
>0=loga1,∴a> .
.
当 <a<1时,f(x)在[1,2]上是减函数,有f(2)=
<a<1时,f(x)在[1,2]上是减函数,有f(2)=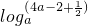 >0=loga1,
>0=loga1,
∴4a-2+ <1,a<
<1,a< .故有
.故有  <a<
<a< .
.
综上,a> 或
或  <a<
<a< .
.
故选:C.
点评:本题主要考查对数函数的单调性和特殊点,二次函数的性质,复合函数的单调性,体现了分类讨论的数学思想.
分析:设
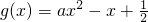 ,由g(x)>0,可得a>
,由g(x)>0,可得a> ,故a>
,故a> ,g(x)在[1,2]上是递增函数.当a>1时,f(x)在[1,2]上是增函数,根据f(1)>0求出a的取值范围;当
,g(x)在[1,2]上是递增函数.当a>1时,f(x)在[1,2]上是增函数,根据f(1)>0求出a的取值范围;当 <a<1时,f(x)在[1,2]上是减函数,由f(2)>0求出a的取值范围,最后把这两个范围取并集.
<a<1时,f(x)在[1,2]上是减函数,由f(2)>0求出a的取值范围,最后把这两个范围取并集.解答:设
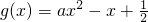 ,由
,由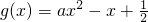 >0,可得 a>
>0,可得 a> .
.当1≤x≤2时,
 的最大值为
的最大值为 ,从而a>
,从而a> .
.在a>
 的前提下,易知函数g(x)的对称轴x=
的前提下,易知函数g(x)的对称轴x= 在区间[1,2]的左边,
在区间[1,2]的左边,从而g(x)在[1,2]上是递增函数.
当a>1时,f(x)在[1,2]上是增函数,有f(1)=
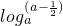 >0=loga1,∴a>
>0=loga1,∴a> .
.当
 <a<1时,f(x)在[1,2]上是减函数,有f(2)=
<a<1时,f(x)在[1,2]上是减函数,有f(2)=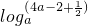 >0=loga1,
>0=loga1,∴4a-2+
 <1,a<
<1,a< .故有
.故有  <a<
<a< .
.综上,a>
 或
或  <a<
<a< .
.故选:C.
点评:本题主要考查对数函数的单调性和特殊点,二次函数的性质,复合函数的单调性,体现了分类讨论的数学思想.

练习册系列答案
相关题目
 在[1,2]上的值恒为正,则a的取值范围是( )
在[1,2]上的值恒为正,则a的取值范围是( ) B.
B. C.
C. D.
D.
 在[1,2]上的值恒为正,则a的取值范围是( )
在[1,2]上的值恒为正,则a的取值范围是( ) B.
B. C.
C. D.
D.
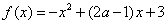 在[1,2]上的值恒为正,则a的取值范围是( )
在[1,2]上的值恒为正,则a的取值范围是( ) B.
B.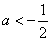 C.
C. D.
D.