题目内容
3.设函数y=f(x)的定义域为D,如果存在非零常数T,对于任意x∈D,都有f(x+T)=T•f(x),则称函数y=f(x)是“似周期函数”,非零常数T为函数y=f(x)的“似周期”.现有下面四个关于“似周期函数”的命题:①如果“似周期函数”y=f(x)的“似周期”为-1,那么它是周期为2的周期函数;②函数f(x)=x是“似周期函数”; ③函数f(x)=2-x是“似周期函数”; ④如果函数f(x)=cosωx是“似周期函数”,那么“ω=kπ,k∈Z”.其中真命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由题意,首先理解似周期函数的定义,从而解得.
解答 解:①如果“似周期函数”y=f(x)的“似周期”为-1,
则f(x-1)=-f(x),即f(x-1)=-f(x)=-(-f(x+1))=f(x+1);
故它是周期为2的周期函数;故①正确,;
②对于“似周期”为T的函数y=f(x),若f(T)>0,则f(2015T)=T2014′f(T)>0;故②正确,
③若函数f(x)=x是“似周期函数”,
则存在非零常数T,使f(x+T)=T•f(x),
即x+T=Tx;故(1-T)x+T=0恒成立;
故不存在T.故假设不成立,故③错误;
④若函数f(x)=2-x是“似周期函数”,
则存在非零常数T,使f(x+T)=T•f(x),
即2-x-T=T•2-x,
即(T-2-T)•2-x=0;
而令y=x-2-x,作图象如下,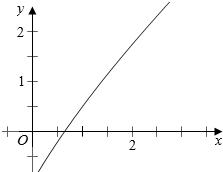
故存在T>0,使T-2-T=0;故④正确;
⑤若函数f(x)=cosωx是“似周期函数”,
则存在非零常数T,使f(x+T)=T•f(x),
即cos(ωx+ωT)=Tcosωx;
故T=1或T=-1;
故“ω=kπ,k∈Z”.故⑤正确;
故选:D.
点评 本题主要考查与函数有关的命题的真假判断,正确理解似周期函数的定义是解决本题的关键.

练习册系列答案
相关题目
14.下列四组数:(1)$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$; (2)2,$-2\sqrt{2}$,4;(3)a2,a4,a8;(4)lg2,lg4,lg8;那么( )
| A. | (1)是等差数列,(2)是等比数列 | B. | (2)和(3)是等比数列 | ||
| C. | (3)是等比数列,(4)是等差数列 | D. | (2)是等比数列,(4)是等差数列 |
18.已知正项等比数列{an}满足:a7=a6+2a5,若存在两项am,an使得$\sqrt{{a}_{m}{a}_{n}}$=4a1,则$\frac{1}{m}$+$\frac{5}{n}$的最小值为( )
| A. | $1+\frac{{\sqrt{5}}}{3}$ | B. | $\frac{7}{4}$ | C. | 2 | D. | $\frac{11}{4}$ |
12.在公比为q的等比数列{an}中,若5a4=1,a5=5,则q等于( )
| A. | $\frac{1}{25}$ | B. | $\frac{1}{5}$ | C. | 5 | D. | 25 |
