题目内容
分段函数f(x)=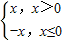 可以表示为f(x)=|x|,同样分段函数f(x)=
可以表示为f(x)=|x|,同样分段函数f(x)=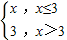 可以表示为f(x)=
可以表示为f(x)= (x+3-|x-3|),仿此,分段函数f(x)=
(x+3-|x-3|),仿此,分段函数f(x)=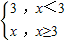 可以表示为f(x)= ,分段函数f(x)=
可以表示为f(x)= ,分段函数f(x)=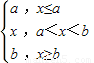 可以表示为f(x)= .
可以表示为f(x)= .
【答案】分析:由类比推理的特点,读懂已知仿照例子可得.
解答:解:由题意可得分段函数f(x)=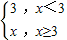 可以表示为:
可以表示为:
f(x)= (3+x-|3-x|)=
(3+x-|3-x|)= (x+3-|x-3|);
(x+3-|x-3|);
分段函数f(x)=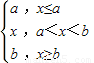 可以表示为:
可以表示为:
f(x)= (a+b+|x-a|-|x-b|),
(a+b+|x-a|-|x-b|),
故答案为: (x+3-|x-3|);
(x+3-|x-3|); (a+b+|x-a|-|x-b|)
(a+b+|x-a|-|x-b|)
点评:本题考查类比推理,由已知得出式子的实质是解决问题的关键,属基础题.
解答:解:由题意可得分段函数f(x)=
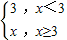 可以表示为:
可以表示为:f(x)=
 (3+x-|3-x|)=
(3+x-|3-x|)= (x+3-|x-3|);
(x+3-|x-3|);分段函数f(x)=
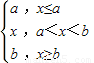 可以表示为:
可以表示为:f(x)=
 (a+b+|x-a|-|x-b|),
(a+b+|x-a|-|x-b|),故答案为:
 (x+3-|x-3|);
(x+3-|x-3|); (a+b+|x-a|-|x-b|)
(a+b+|x-a|-|x-b|)点评:本题考查类比推理,由已知得出式子的实质是解决问题的关键,属基础题.

练习册系列答案
相关题目
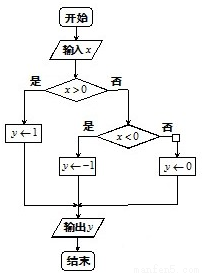
 (2009•普陀区二模)如图是某算法的程序框图,该算法可表示分段函数,则其输出结果所表示的分段函数为f(x)=
(2009•普陀区二模)如图是某算法的程序框图,该算法可表示分段函数,则其输出结果所表示的分段函数为f(x)=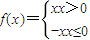 可以表示为f(x)=|x|,分段函数
可以表示为f(x)=|x|,分段函数 可表示为
可表示为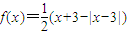 ,仿此,分段函数
,仿此,分段函数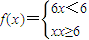 可以表示为f(x)= .
可以表示为f(x)= .