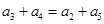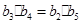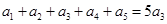题目内容
用类比推理的方法填表:
| 等差数列{an}中 | 等比数列{bn}中 |
| a3+a4=a2+a5 | b3•b4=b2•b5 |
| a1+a2+a3+a4+a5=5a3 | b1b2b3b4b5=b35 b1b2b3b4b5=b35 |
分析:由于表格左右均为等差数列的性质,表格右边均为等比数列的性质,左边的加法可类比推理到右边的乘法,而左边的乘法可类比到右边的乘方.
解答:解:由等差数列的性质,a3+a4=a2+a5,与等比数列的性质b3•b4=b2•b5,可得等差数列的加法性质可类比推断出等比数列的乘法性质,
则a1+a2+a3+a4+a5=5a3=a3+a3+a3+a3+a3,
类比推断出在等比数列中
b1b2b3b4b5=b3•b3•b3•b3•b3=b35
故答案为:b1b2b3b4b5=b35
则a1+a2+a3+a4+a5=5a3=a3+a3+a3+a3+a3,
类比推断出在等比数列中
b1b2b3b4b5=b3•b3•b3•b3•b3=b35
故答案为:b1b2b3b4b5=b35
点评:本题考查的知识点是推理,等比数列的性质,其中由等差数列的性质类比到等比数列的性质往往运算上高一个等级

练习册系列答案
相关题目
用类比推理的方法填表:
| 等差数列{an}中 | 等比数列{bn}中 |
| a3+a4=a2+a5 | b3•b4=b2•b5 |
| a1+a2+a3+a4+a5=5a3 |
用类比推理的方法填表:
等差数列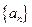 中 中 | 等比数列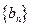 中 中 |
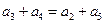 | 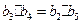 |
 | |
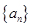 中
中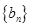 中
中