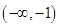题目内容
(本题满分12分)已知函数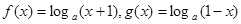 ,
,
其中(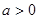 且
且
⑴求函数 的定义域;
的定义域;
⑵判断函数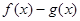 的奇偶性,并予以证明;
的奇偶性,并予以证明;
⑶判断它在区间(0,1)上的单调性并说明理由。
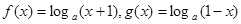 ,
,其中(
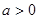 且
且
⑴求函数
 的定义域;
的定义域; ⑵判断函数
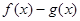 的奇偶性,并予以证明;
的奇偶性,并予以证明; ⑶判断它在区间(0,1)上的单调性并说明理由。
⑴  ;⑵
;⑵ 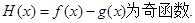
⑶区间(0,1)上为单调递增函数。
 ;⑵
;⑵ 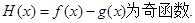
⑶区间(0,1)上为单调递增函数。
(1)函数f(x)+g(x)的定义域应该是f(x),g(x)定义域的交集即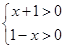 ,
,
,所以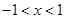 ,即所求函数的定义域为(-1,1).
,即所求函数的定义域为(-1,1).
(2)由(1)知其定义域关于原点对称,并且根据对数的运算性质可得 ,
,
然后再根据奇偶函数的定义判断出H(-x)=-H(x),从而可知 为奇函数。
为奇函数。
(3)利用单调性的定义第一步取值:任取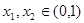 且
且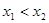 ;
;
第二步:作差变形判断 的符号,再判断时要利用对数函数的性质,
的符号,再判断时要利用对数函数的性质,
第三步:得出结论。
⑴ 由题意得: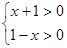
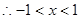
所以所求定义域为
⑵ 令
则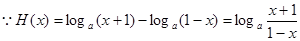
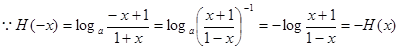
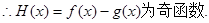
⑶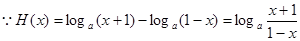 ,
,
任取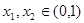 且
且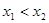 ,则
,则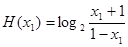 ,
,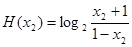
则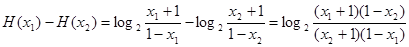
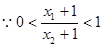 ,
,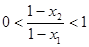 ,
,
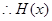 在区间(0,1)上为单调递增函数。
在区间(0,1)上为单调递增函数。
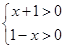 ,
,,所以
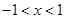 ,即所求函数的定义域为(-1,1).
,即所求函数的定义域为(-1,1).(2)由(1)知其定义域关于原点对称,并且根据对数的运算性质可得
 ,
,然后再根据奇偶函数的定义判断出H(-x)=-H(x),从而可知
 为奇函数。
为奇函数。(3)利用单调性的定义第一步取值:任取
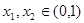 且
且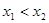 ;
;第二步:作差变形判断
 的符号,再判断时要利用对数函数的性质,
的符号,再判断时要利用对数函数的性质,第三步:得出结论。
⑴ 由题意得:
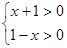
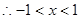
所以所求定义域为

⑵ 令

则
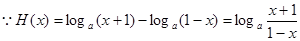
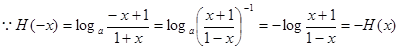
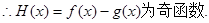
⑶
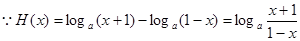 ,
,任取
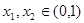 且
且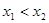 ,则
,则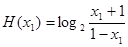 ,
,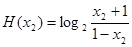
则
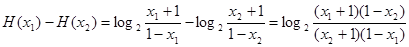
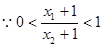 ,
,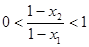 ,
,
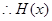 在区间(0,1)上为单调递增函数。
在区间(0,1)上为单调递增函数。
练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
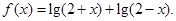
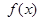 的定义域;
的定义域;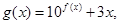 求函数
求函数 的值域.
的值域.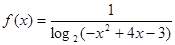 的定义域为( )
的定义域为( )
 的定义域为 .
的定义域为 .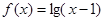 的定义域是
的定义域是 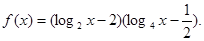
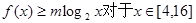 恒成立,求m的取值范围.
恒成立,求m的取值范围. 的定义域是__________________ (用集合或区间表示).
的定义域是__________________ (用集合或区间表示).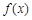 的定义域为
的定义域为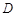 ,若存在非零实数
,若存在非零实数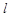 使得对于任意
使得对于任意 ,有
,有 ,且
,且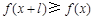 ,则称
,则称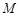 上的“高调函数”.现给出下列命题:
上的“高调函数”.现给出下列命题: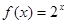 为
为 上的“1高调函数”;
上的“1高调函数”;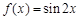 为
为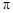 高调函数”;
高调函数”;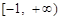 的函数
的函数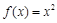 为
为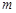 高调函数”,那么实数
高调函数”,那么实数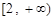 ;
; 的定义域是
的定义域是