题目内容
二面角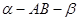 的平面角是锐角,点C
的平面角是锐角,点C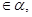 且点C不在棱AB上,D是C在平面
且点C不在棱AB上,D是C在平面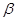 上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
A .∠CEB>∠DEB B.∠CEB=∠DEB
C.∠CEB<∠DEB D.∠CEB与∠DEB的大小关系不能确定
【答案】
A.
【解析】
试题分析:因为 ,因为
,因为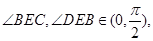
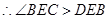 .
.
考点:二面角,线面角,余弦函数的单调性.
点评:解本小题用到了一个重要的结论:平面内的一条直线与这个平面的斜线所成的角的余弦值等于这条直线与这条斜线在这个平面内的射影所成的角的余弦值乘以斜线与平面所成的角的余弦,据此可得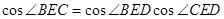 ,因为0<
,因为0<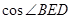 <1,所以
<1,所以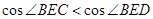 ,再利用余弦函数的单调性即可得到∠CEB>∠DEB.
,再利用余弦函数的单调性即可得到∠CEB>∠DEB.

练习册系列答案
相关题目
 的平面角是锐角
的平面角是锐角 ,
, 内一点
内一点 到
到 的距离为3,点C到棱
的距离为3,点C到棱 的距离为4,那么
的距离为4,那么 的值等于( )
的值等于( ) B.
B. C.
C.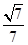 D.
D.
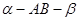 的平面角是锐角,点C
的平面角是锐角,点C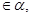 且点C不在棱AB上,D是C在平面
且点C不在棱AB上,D是C在平面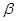 上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )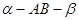 的平面角是锐角
的平面角是锐角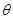 ,平面
,平面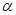 内有一点
内有一点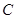 到
到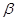 的距离为3,点
的距离为3,点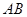 距离为4,那么
距离为4,那么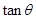 =
=
 的平面角是锐角
的平面角是锐角 ,
, 内一点
内一点 到
到 的距离为3,点C到棱
的距离为3,点C到棱 的距离为4,那么
的距离为4,那么 的值等于
的值等于  B、
B、 C、
C、 D、
D、