题目内容
设不等式组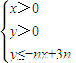 所表示的平面区域为Dn,记Dn内的整点个数为an(n∈N*)(整点即横坐标与纵坐标均为整数的点).
所表示的平面区域为Dn,记Dn内的整点个数为an(n∈N*)(整点即横坐标与纵坐标均为整数的点).(1)求数列{an}的通项公式;
(2)(理)设
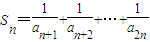 ,求Sn的最小值(n>1,n∈N*);
,求Sn的最小值(n>1,n∈N*);(3)设
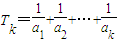 求证:
求证: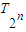 ≥
≥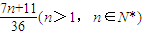 .
.(文)记数列{an}的前n项和为Sn,且
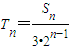 .若对一切的正整数n,总有Tn≤m,求实数m的取值范围.
.若对一切的正整数n,总有Tn≤m,求实数m的取值范围.
【答案】分析:(1)由题设知Dn内的整点在直线x=1和x=2上.记直线y=-nx+3n为l,l与直线x=1和x=2的交点的纵坐标分别为y1、y2,由y1=2n,y2=n,知an=3n(n∈N*).
(2)(理)(i)由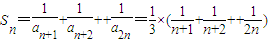 .知
.知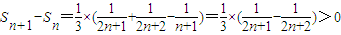 .所以
.所以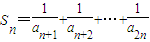 ≥
≥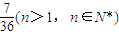 .
.
(ii)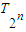 =
=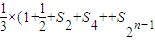 )≥
)≥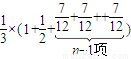 =
=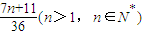 .
.
(文)由题设知Tn=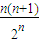 .Tn+1-Tn=
.Tn+1-Tn=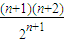 -
-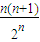 =
=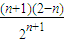 ,n≥3时{Tn}是递减数列,且
,n≥3时{Tn}是递减数列,且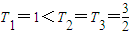 ,所以T2,T3是数列{Tn}的最大项,故m≥
,所以T2,T3是数列{Tn}的最大项,故m≥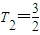 .
.
解答:解:(1)∵x>0,y=3n-nx>0,0<x<3,x=1或x=2.
∴Dn内的整点在直线x=1和x=2上.记直线y=-nx+3n为l,l与直线x=1和x=2的交点的纵坐标分别为y1、y2,
∴y1=2n,y2=n.∴an=3n(n∈N*).
(2)(理)(i)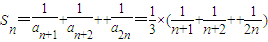 .
.
∵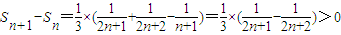 .
.
∴Sn+1>Sn,Sn≥S2(n>1,n∈N*).
∵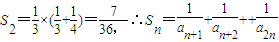 ≥
≥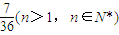 .
.
(ii)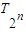 =
=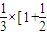
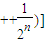 =
=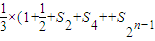 )
)
≥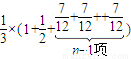 =
=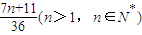 .
.
(文)∵Sn=3(1+2+3+…+n)=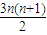 ,∴Tn=
,∴Tn=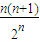 .
.
∴Tn+1-Tn=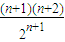 -
-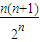 =
=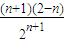 ,∴当n≥3时,Tn+1<Tn,∴n≥3时{Tn}是递减数列,且
,∴当n≥3时,Tn+1<Tn,∴n≥3时{Tn}是递减数列,且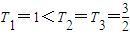 ,∴T2,T3是数列{Tn}的最大项,故m≥
,∴T2,T3是数列{Tn}的最大项,故m≥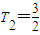
点评:本题考查数列的性质和应用,解题时要注意公式的合理运用和不等式的应用.
(2)(理)(i)由
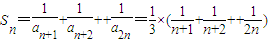 .知
.知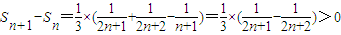 .所以
.所以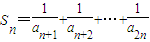 ≥
≥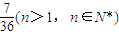 .
.(ii)
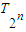 =
=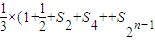 )≥
)≥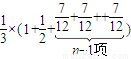 =
=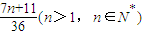 .
.(文)由题设知Tn=
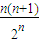 .Tn+1-Tn=
.Tn+1-Tn=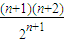 -
-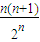 =
=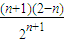 ,n≥3时{Tn}是递减数列,且
,n≥3时{Tn}是递减数列,且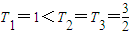 ,所以T2,T3是数列{Tn}的最大项,故m≥
,所以T2,T3是数列{Tn}的最大项,故m≥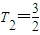 .
.解答:解:(1)∵x>0,y=3n-nx>0,0<x<3,x=1或x=2.
∴Dn内的整点在直线x=1和x=2上.记直线y=-nx+3n为l,l与直线x=1和x=2的交点的纵坐标分别为y1、y2,
∴y1=2n,y2=n.∴an=3n(n∈N*).
(2)(理)(i)
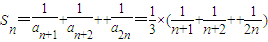 .
.∵
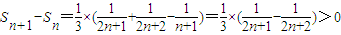 .
.∴Sn+1>Sn,Sn≥S2(n>1,n∈N*).
∵
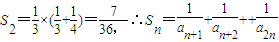 ≥
≥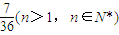 .
.(ii)
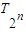 =
=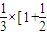
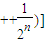 =
=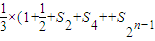 )
)≥
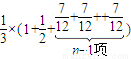 =
=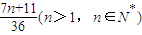 .
.(文)∵Sn=3(1+2+3+…+n)=
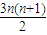 ,∴Tn=
,∴Tn=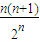 .
.∴Tn+1-Tn=
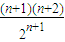 -
-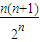 =
=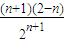 ,∴当n≥3时,Tn+1<Tn,∴n≥3时{Tn}是递减数列,且
,∴当n≥3时,Tn+1<Tn,∴n≥3时{Tn}是递减数列,且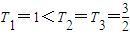 ,∴T2,T3是数列{Tn}的最大项,故m≥
,∴T2,T3是数列{Tn}的最大项,故m≥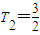
点评:本题考查数列的性质和应用,解题时要注意公式的合理运用和不等式的应用.

练习册系列答案
相关题目
 所表示的平面区域内的概率.
所表示的平面区域内的概率.