题目内容
已知抛物线过点A(-1,0),B(1,0),且以圆x2+y2=4的切线为准线,则抛物线的焦点的轨迹方程( )A.
 +
+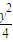 =1(y≠0)
=1(y≠0)B.
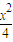 +
+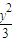 =1(y≠0)
=1(y≠0)C.
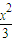 -
-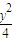 =1(y≠0)
=1(y≠0)D.
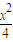 -
-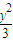 =1(y≠0)
=1(y≠0)
【答案】分析:设出切线方程,表示出圆心到切线的距离求得a和b的关系,再设出焦点坐标,根据抛物线的定义求得点A,B到准线的距离等于其到焦点的距离,然后两式平方后分别相加和相减,联立后,即可求得x和y的关系式.
解答:解:设切线ax+by-1=0,则圆心到切线距离等于半径
∴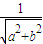 =2
=2
∴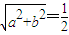 ,
,
∴a2+b2=
设抛物线焦点为(x,y),根据抛物线定义可得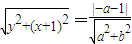
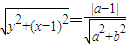
平方相加得:x2+1+y2=4(a2+1)①
平方相减得:x=4a,
∴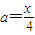 ②
②
把②代入①可得:x2+1+y2=4(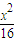 +1)
+1)
即: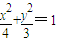
∵焦点不能与A,B共线
∴y≠0
∴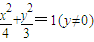
∴抛物线的焦点轨迹方程为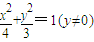
故选B.
点评:本题以圆为载体,考查抛物线的定义,考查轨迹方程,解题时利用圆的切线性质,抛物线的定义是关键.
解答:解:设切线ax+by-1=0,则圆心到切线距离等于半径
∴
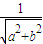 =2
=2∴
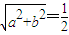 ,
,∴a2+b2=

设抛物线焦点为(x,y),根据抛物线定义可得
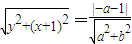
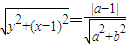
平方相加得:x2+1+y2=4(a2+1)①
平方相减得:x=4a,
∴
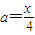 ②
②把②代入①可得:x2+1+y2=4(
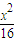 +1)
+1)即:
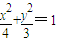
∵焦点不能与A,B共线
∴y≠0
∴
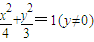
∴抛物线的焦点轨迹方程为
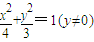
故选B.
点评:本题以圆为载体,考查抛物线的定义,考查轨迹方程,解题时利用圆的切线性质,抛物线的定义是关键.

练习册系列答案
相关题目
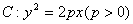 过点A(1,-2)。
过点A(1,-2)。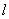 ,使得直线
,使得直线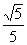 ?若存在,求出直线
?若存在,求出直线