题目内容
已知cos =
= ,0<α<
,0<α< ,则sin
,则sin =________.
=________.
【答案】
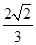
【解析】由已知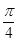 <α+
<α+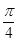 <
<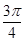 ,∴sin
,∴sin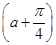 >0,
>0,
∴sin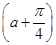 =
=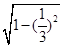 =
=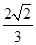 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
已知cos =
= ,0<α<
,0<α< ,则sin
,则sin =________.
=________.
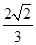
【解析】由已知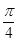 <α+
<α+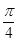 <
<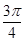 ,∴sin
,∴sin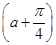 >0,
>0,
∴sin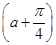 =
=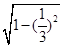 =
=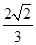 .
.

 名校课堂系列答案
名校课堂系列答案