题目内容
若在区间[1,4]内任取实数a,在区间[0,3]内任取实数b,则方程ax2+2x+b=0有实根的概率为
- A.

- B.

- C.
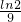
- D.
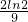
D
分析:先把方程ax2+2x+b=0有实根,转化为△=4-4ab≥0,进而得b≤ .,再画出图象,利用面积比来计算概率即可.
.,再画出图象,利用面积比来计算概率即可.
解答:方程ax2+2x+b=0有实根,等价于△=4-4ab≥0?ab≤1?b≤ .
.
画出对应图象如下:
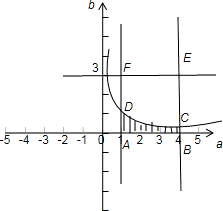 因为∫14
因为∫14 dx=2ln2.
dx=2ln2.
故所求概率p=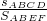 =
=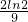 .
.
故选 D.
点评:本题主要考查二次函数的性质以及几何概型和数形结合思想,是对知识点的综合考查,属于中档题.
分析:先把方程ax2+2x+b=0有实根,转化为△=4-4ab≥0,进而得b≤
 .,再画出图象,利用面积比来计算概率即可.
.,再画出图象,利用面积比来计算概率即可.解答:方程ax2+2x+b=0有实根,等价于△=4-4ab≥0?ab≤1?b≤
 .
.画出对应图象如下:
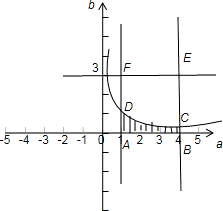 因为∫14
因为∫14 dx=2ln2.
dx=2ln2.故所求概率p=
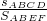 =
=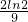 .
.故选 D.
点评:本题主要考查二次函数的性质以及几何概型和数形结合思想,是对知识点的综合考查,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目