题目内容
13．曲线y=$\frac{1}{2}$x2-1在点（1，-$\frac{1}{2}$）处切线的倾斜角为（ ）| A． | $\frac{π}{4}$ | B． | -$\frac{π}{4}$ | C． | 1 | D． | -$\frac{1}{2}$ |
分析 求出函数的导数，求得切线的斜率，结合直线的斜率公式，由倾斜角的范围，即可得到所求值．
解答 解：y=$\frac{1}{2}$x2-1的导数为y′=x，
即有在点（1，-$\frac{1}{2}$）处切线的斜率为k=1，
由直线的斜率公式k=tanα（α为倾斜角），
即有tanα=1，
由于0≤α＜π，
可得α=$\frac{π}{4}$，
故选：A．
点评 本题考查导数的运用：求切线的斜率，主要考查导数的几何意义，同时考查直线的斜率公式和倾斜角的大小，属于基础题．
练习册系列答案
备战中考寒假系列答案
相关题目
18．a，b≥1，a≠b，下列各数中最大的是（ ）
| A． | $\frac{1}{2}$（a+b） | B． | $\frac{2ab}{a+b}$ | C． | $\frac{1}{2}$（$\frac{1}{a}$+$\frac{1}{b}$） | D． | $\sqrt{ab}$ |
在如图所示的正方体ABCD-A1B1C1D1中，
如图，已知PA⊥平面ABCD，ABCD为矩形，M、N为AB、PC的中点．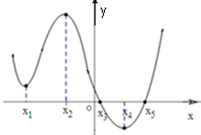
如图是导函数y=f′（x）的图象，在标记的点中，在哪一点处