题目内容
(1)求证:a5+b5≥a2b3+a3b2,(a,b∈R+);
(2)用反证法证明:若a,b,c均为实数,且a=x2-2y+
,b=y2-2z+
,c=z2-2x+
,求证a,b,c中至少有一个大于0.
(2)用反证法证明:若a,b,c均为实数,且a=x2-2y+
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
分析:(1)化简a5+b5-( a2b3+a3b2 )等于 (a3-b3)(a2-b2),分a≥b>0时和b≥a>0时两种情况,都能推出(a3-b3)(a2-b2)≥0,从而证得不等式成立.
(2)假设a、b、c都小于或等于0,则有a+b+c=(x-1)2+(y-1)2+(z-1)2+π-3≤0,得出矛盾,可得假设不成立,命题得证.
(2)假设a、b、c都小于或等于0,则有a+b+c=(x-1)2+(y-1)2+(z-1)2+π-3≤0,得出矛盾,可得假设不成立,命题得证.
解答:证明:(1)∵a,b∈R+,且a5+b5-( a2b3+a3b2 )=a2(a3-b3)+b2(b3-a3)=(a3-b3)(a2-b2),
当a≥b>0时,(a3-b3)≥0,(a2-b2)≥0,∴(a3-b3)(a2-b2)≥0,
故 a5+b5≥a2b3+a3b2 .
当b≥a>0时,(a3-b3)≤0,(a2-b2)≤0,∴(a3-b3)(a2-b2)≥0,
故 a5+b5≥a2b3+a3b2 .
(2)假设a、b、c都小于或等于0,则有a+b+c=(x-1)2+(y-1)2+(z-1)2+π-3≤0,
故 (x-1)2+(y-1)2+(z-1)2≤3-π<0,矛盾,故假设不成立,
即a,b,c中至少有一个大于0.
当a≥b>0时,(a3-b3)≥0,(a2-b2)≥0,∴(a3-b3)(a2-b2)≥0,
故 a5+b5≥a2b3+a3b2 .
当b≥a>0时,(a3-b3)≤0,(a2-b2)≤0,∴(a3-b3)(a2-b2)≥0,
故 a5+b5≥a2b3+a3b2 .
(2)假设a、b、c都小于或等于0,则有a+b+c=(x-1)2+(y-1)2+(z-1)2+π-3≤0,
故 (x-1)2+(y-1)2+(z-1)2≤3-π<0,矛盾,故假设不成立,
即a,b,c中至少有一个大于0.
点评:本题主要考查用比较法证明不等式,用反证法证明不等式,体现了分类讨论的数学而思想,属于中档题.

练习册系列答案
相关题目
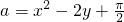 ,
,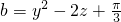 ,
,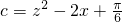 ,求证a,b,c中至少有一个大于0.
,求证a,b,c中至少有一个大于0.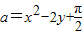 ,
,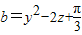 ,
,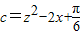 ,求证a,b,c中至少有一个大于0.
,求证a,b,c中至少有一个大于0. ,
,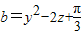 ,
,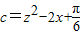 ,求证a,b,c中至少有一个大于0.
,求证a,b,c中至少有一个大于0.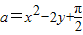 ,
,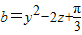 ,
,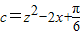 ,求证a,b,c中至少有一个大于0.
,求证a,b,c中至少有一个大于0.