题目内容
已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.

(1)若该四棱锥的左视图为直角三角形,则它的体积为__________;
(2)关于该四棱锥的下列结论中:
①四棱锥中至少有两组侧面互相垂直;
②四棱锥的侧面中可能存在三个直角三角形;
③四棱锥中不可能存在四组互相垂直的侧面.
所有正确结论的序号是___________.
【答案】
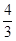 ;①②③
;①②③
【解析】
试题分析:(1)左视图为直角三角形时直角三角形的斜边为2,则斜边上的高为1,此高即为四棱锥的高,所以此四棱锥的体积为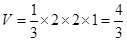 .
.
(2)此棱锥的直观图如图所示,底面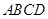 为正方形,侧面
为正方形,侧面 .
.
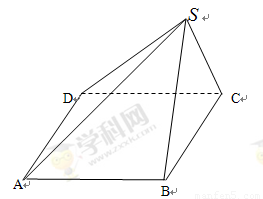
由面面垂直的性质定理可得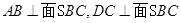 ,因为
,因为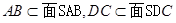 ,所以
,所以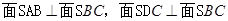 ,故①正;
,故①正;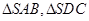 均为直角三角形,
均为直角三角形,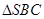 可能为直角三角形.故②正确;假设存在四组互相垂直的侧面,则每组对面互相平行而不能构成棱锥,则假设不成立,故③正确,综上可得正确结论的序号是①②③.
可能为直角三角形.故②正确;假设存在四组互相垂直的侧面,则每组对面互相平行而不能构成棱锥,则假设不成立,故③正确,综上可得正确结论的序号是①②③.
考点:三视图,面面垂直.

练习册系列答案
相关题目
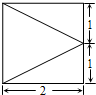 已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.
已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.