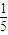题目内容
(理科)设点A(1,2),B(2,1)如果直线ax+by=1与线段AB有一个公共点,那么a2+b2( )
分析:由题意得:点A(1,2),B(2,1)在直线ax+by=1的两侧(或过A,或过B),那么把这两个点代入ax+by=1,它们的符号相反,乘积小于等于0,即可得出关于a,b的不等关系,画出此不等关系表示的平面区域,结合线性规划思想求出a2+b2的最小值.
解答: 解:∵直线ax+by=1与线段AB有一个公共点,
解:∵直线ax+by=1与线段AB有一个公共点,
∴点A(1,2),B(2,1)在直线ax+by=1的两侧(或过A,或过B),
∴(a+2b-1)(2a+b-1)≤0,
画出它们表示的平面区域,如图所示.
a2+b2表示原点到区域内的点的距离的平方,
由图可知,当原点O到直线2a+b-1=0的距离为原点到区域内的点的距离的最小值,即
∴a2+b2的最小值为
故选C.
 解:∵直线ax+by=1与线段AB有一个公共点,
解:∵直线ax+by=1与线段AB有一个公共点,∴点A(1,2),B(2,1)在直线ax+by=1的两侧(或过A,或过B),
∴(a+2b-1)(2a+b-1)≤0,
画出它们表示的平面区域,如图所示.
a2+b2表示原点到区域内的点的距离的平方,
由图可知,当原点O到直线2a+b-1=0的距离为原点到区域内的点的距离的最小值,即
| 1 | ||
|
∴a2+b2的最小值为
| 1 |
| 5 |
故选C.
点评:本题考查线性规划的应用,本题解题的关键是写出约束条件,画出可行域,属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目


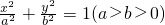 上一点,F1、F2是椭圆的两个焦点,且满足|AF1|+|AF2|=4.
上一点,F1、F2是椭圆的两个焦点,且满足|AF1|+|AF2|=4.