题目内容
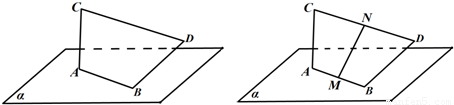
随着环保理念的深入,用建筑钢材余料创作城市雕塑逐渐流行.下图是其中一个抽象派雕塑的设计图.图中α表示水平地面,线段AB表示的钢管固定在α上;为了美感,需在焊接时保证:线段AC表示的钢管垂直于α,BD⊥AB,且保持BD与AC异面.(1)若收集到的余料长度如下:AC=BD=24(单位长度),AB=7,CD=25,按现在手中的材料,求BD与α应成的角;
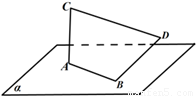
(2)设计师想在AB,CD中点M,N处再焊接一根连接管,然后挂一个与AC,BD同时平
行的平面板装饰物.但他担心此设计不一定能实现.请你替他打消疑虑:无论AB,CD多长,焊接角度怎样,一定存在一个过MN的平面与AC,BD同时平行(即证明向量
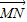 与
与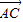 ,
,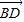 共面,写出证明过程);
共面,写出证明过程);(3)如果事先能收集确定的材料只有AC=BD=24,请替设计师打消另一个疑虑:即MN要准备多长不用视AB,CD长度而定,只与θ有关(θ为设计的BD与α所成的角),写出MN与θ的关系式,并帮他算出无论如何设计MN都一定够用的长度.
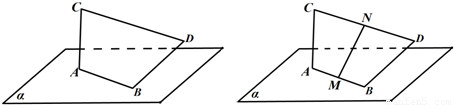
【答案】分析:(1)设D在α上的射影为H,过D作DK⊥AC于K,可得AHDK为矩形,计算DH,即可求得BD与α所成的角是30°.
(2)由共面向量的判定定理得到量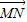 与
与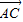 ,
,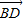 共面,即可得到结论;
共面,即可得到结论;
(3)由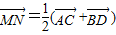 ,求模长,即可得到结论.
,求模长,即可得到结论.
解答:解:(1)设D在α上的射影为H

∵AC⊥α,DH⊥α,∴AC∥∥DH,∴AC,DH共面,
∴过D作DK⊥AC于K,
∴AHDK为矩形,
设DH=h,则(AC-h)2+AH2=CD2,①
由三垂线定理易知BH⊥AB
∴AH2=AB2+BH2=AB2+(BD2-h2)②
将②代入①,得:(24-h)2+72+(242-h2)=252,解得h=12,
于是sin∠DBH= ,
,
∴∠DBH=30°,即BD与α所成的角是30°.
(2)由向量加法的三角形法则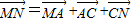 ,
,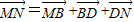 ,
,
两式相加即得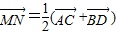 .
.
∴由共面向量的判定定理得到量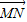 与
与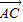 ,
, 共面.
共面.
从而一定存在一个过MN的平面与AC,BD同时平行
(3)∵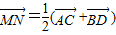
∴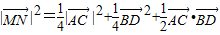 =288(1+sinθ)(单位长度)
=288(1+sinθ)(单位长度)
∵θ∈(0,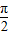 ),
),
∴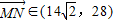 ,即MN准备28(单位长度)就一定够用.
,即MN准备28(单位长度)就一定够用.
点评:本题考查线面角,考查向量知识的运用,考查学生的计算能力,属于中档题.
(2)由共面向量的判定定理得到量
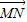 与
与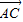 ,
,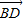 共面,即可得到结论;
共面,即可得到结论;(3)由
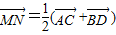 ,求模长,即可得到结论.
,求模长,即可得到结论.解答:解:(1)设D在α上的射影为H

∵AC⊥α,DH⊥α,∴AC∥∥DH,∴AC,DH共面,
∴过D作DK⊥AC于K,
∴AHDK为矩形,
设DH=h,则(AC-h)2+AH2=CD2,①
由三垂线定理易知BH⊥AB
∴AH2=AB2+BH2=AB2+(BD2-h2)②
将②代入①,得:(24-h)2+72+(242-h2)=252,解得h=12,
于是sin∠DBH=
 ,
,∴∠DBH=30°,即BD与α所成的角是30°.
(2)由向量加法的三角形法则
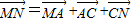 ,
,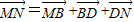 ,
,两式相加即得
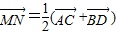 .
.∴由共面向量的判定定理得到量
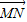 与
与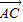 ,
, 共面.
共面.从而一定存在一个过MN的平面与AC,BD同时平行
(3)∵
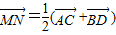
∴
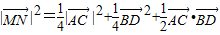 =288(1+sinθ)(单位长度)
=288(1+sinθ)(单位长度)∵θ∈(0,
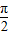 ),
),∴
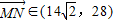 ,即MN准备28(单位长度)就一定够用.
,即MN准备28(单位长度)就一定够用.点评:本题考查线面角,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
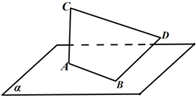 随着环保理念的深入,用建筑钢材余料创作城市雕塑逐渐流行.如图是其中一个抽象派雕塑的设计图.图中α表示水平地面.线段AB表示的钢管固定在α上;为了美感,需在焊接时保证:线段AC表示的钢管垂直于α,BD⊥AB,且保持BD与AC异面.若收集到的余料长度如下:AC=BD=24(单位长度),AB=7,CD=25,按现在手中的材料和设计要求,求BD与α应成的角.
随着环保理念的深入,用建筑钢材余料创作城市雕塑逐渐流行.如图是其中一个抽象派雕塑的设计图.图中α表示水平地面.线段AB表示的钢管固定在α上;为了美感,需在焊接时保证:线段AC表示的钢管垂直于α,BD⊥AB,且保持BD与AC异面.若收集到的余料长度如下:AC=BD=24(单位长度),AB=7,CD=25,按现在手中的材料和设计要求,求BD与α应成的角.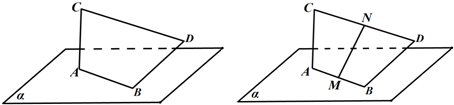
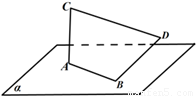
 与
与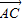 ,
,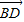 共面,写出证明过程);
共面,写出证明过程);