题目内容
定义:S为R的真子集,?x,y∈S,若x+y∈S,x-y∈S,则称S对加减法封闭.有以下四个命题,请判断真假:①自然数集对加减法封闭;
②有理数集对加减法封闭;
③若有理数集对加减法封闭,则无理数集也对加减法封闭;
④若S1,S2为R的两个真子集,且对加减法封闭,则必存在c∈R,使得c∉S1∪S2;
四个命题中为“真”的是 .(填写序号)
【答案】分析:根据集合S对加减法封闭的定义,举出反例可以说明①③不正确.再结合有理数的定义与性质,可证出②正确,最后通过举例说明命题④是正确的,从而得出正确答案.
解答:解:对于①,因为存在x=1,y=2∈N,使x-y=-1∉N,故自然数集对减法不封闭,所以①不正确;
对于②,因为?x,y∈Q,有x+y∈Q且x-y∈Q成立,故则有理数对加减法封闭,故②正确;
对于③,由前面的讨论知有理数集对加减法封闭,而存在x=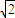 ,y=-
,y=-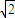 ∈{无理数},使x+y=0∉{无理数},
∈{无理数},使x+y=0∉{无理数},
故无理数集对加减法不封闭,所以③不正确;
对于④,可设S1=Z,S2=Q,它们是R的两个真子集,且对加减法封闭,存在c=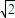 ∈R,且
∈R,且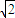 ∉S1∪S2,故④正确.
∉S1∪S2,故④正确.
故答案为:②④
点评:本题以命题真假的判断为载体,考查我们对运算封闭性的理解,着重对自然数、有理数、无理数的运算性质进行了考查,属于基础题.
解答:解:对于①,因为存在x=1,y=2∈N,使x-y=-1∉N,故自然数集对减法不封闭,所以①不正确;
对于②,因为?x,y∈Q,有x+y∈Q且x-y∈Q成立,故则有理数对加减法封闭,故②正确;
对于③,由前面的讨论知有理数集对加减法封闭,而存在x=
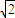 ,y=-
,y=-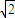 ∈{无理数},使x+y=0∉{无理数},
∈{无理数},使x+y=0∉{无理数},故无理数集对加减法不封闭,所以③不正确;
对于④,可设S1=Z,S2=Q,它们是R的两个真子集,且对加减法封闭,存在c=
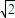 ∈R,且
∈R,且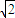 ∉S1∪S2,故④正确.
∉S1∪S2,故④正确.故答案为:②④
点评:本题以命题真假的判断为载体,考查我们对运算封闭性的理解,着重对自然数、有理数、无理数的运算性质进行了考查,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目