题目内容
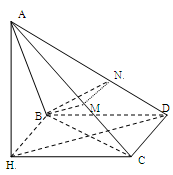
如图示,在四棱锥A-BHCD中,AH⊥面BHCD,此棱锥的三视图如下:
(1)求二面角B-AC-D的余弦弦值;
(2)在线段AC上是否存在一点E,使ED与面BCD成45°角?若存在,确定E的位置;若不存在,说明理由。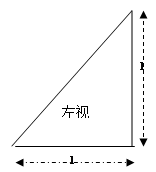

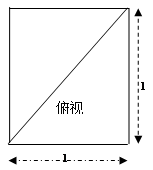
(1)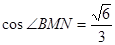 (2)不存在
(2)不存在
解析试题分析:(1)观察三视图,得到边长以及线面关系,取AC的中点
M,过M作MN∥CD交AD于N,则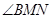 是所求二面角的平面角,
是所求二面角的平面角,
(2)假设存在,把“ED与面BCD成45°角”作为条件,进行计算.
试题解析:(1)由AH⊥面BHCD及三视图知:AH=BH=HC=1,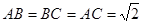 ,
,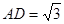 取AC的中点M,过M作MN∥CD交AD于N,则
取AC的中点M,过M作MN∥CD交AD于N,则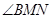 是所求二面角的平面角,
是所求二面角的平面角,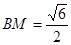 ,
,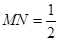 ,
,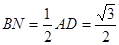
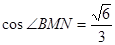 ;
;
(2)假设在线段AC上存在点E合题意,令E在HC上的射影为F,设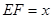 (
(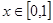 ),则
),则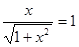 ,矛盾。所以,不存在(注:本题也可用向量法)
,矛盾。所以,不存在(注:本题也可用向量法)
考点:二面角,线面角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为圆
为圆 的直径,
的直径, 为圆周上异于
为圆周上异于 、
、 的一点,
的一点, 垂直于圆
垂直于圆 于
于 ,
, 于点
于点 .
. 平面
平面 ;
; ,
, ,求四面体
,求四面体 的体积.
的体积.
 中,侧棱垂直底面,
中,侧棱垂直底面, ,
, ,
, 是棱
是棱 的中点。
的中点。 ⊥平面
⊥平面
 ,求几何体
,求几何体 的体积。
的体积。
 ,
, ,
, ,
, .又
.又 ,
, ,
, ,直线
,直线 与直线
与直线 所成的角为60°.
所成的角为60°. ;
; 的体积.
的体积.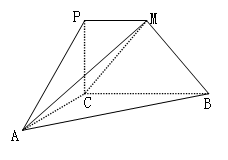
 中,底面
中,底面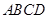 是边长为
是边长为 的正方形,
的正方形,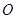 为
为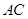 与
与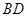 的交点,
的交点,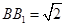 ,
,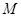 是线段
是线段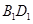 的中点.
的中点.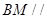 平面
平面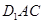 ;
;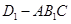 的体积.
的体积.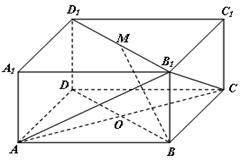
 ,则过A、B的平面中,与球心的最大距离是
,则过A、B的平面中,与球心的最大距离是  ,则正圆锥的侧面积为 .
,则正圆锥的侧面积为 . ,DA⊥平面ABC。AB⊥BC,DA=AB=BC=
,DA⊥平面ABC。AB⊥BC,DA=AB=BC= ,则球O的体积等于 。
,则球O的体积等于 。
 角的平面截球O的表面得到圆C.若圆C的面积等于
角的平面截球O的表面得到圆C.若圆C的面积等于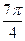 ,则球O的表面积等于 .
,则球O的表面积等于 .