题目内容
17.已知x,y满足约束条件$\left\{\begin{array}{l}x≥1\\ x+y≤3\\ ay≥x-3\end{array}\right.$,若z=2x+y的最小值为1,则a的值是( )| A. | 4 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
分析 由线性约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,求出最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}x≥1\\ x+y≤3\\ ay≥x-3\end{array}\right.$作出可行域如图,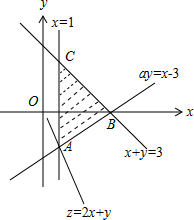
联立$\left\{\begin{array}{l}{x=1}\\{ay=x-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=-\frac{2}{a}}\end{array}\right.$,即A(1,-$\frac{2}{a}$),
化z=2x+y,得y=-2x+z,
由图可知,当直线y=-2x+z过A时,直线在y轴上的截距最小,z有最小值为2×1$-\frac{2}{a}=1$,解得:a=2.
故选:D.
点评 本题考查了简单的线性规划,考查了数形结合及数学转化思想方法,是中档题.

练习册系列答案
相关题目
12.设m=3${∫}_{-1}^{1}$(x2+sinx)}dx,则多项式(x+$\frac{1}{{m\sqrt{x}}}$)6的常数项为( )
| A. | $-\frac{5}{4}$ | B. | $\frac{5}{4}$ | C. | $-\frac{15}{16}$ | D. | $\frac{15}{16}$ |
2.函数f(x)=ax-b的图象如图所示,其中a,b为常数,则下列结论正确的是( )


| A. | a>1,b>0 | B. | a>1,b<0 | C. | 0<a<1,b>0 | D. | 0<a<1,b<0 |
7.已知椭圆mx2+4y2=1的离心率为$\frac{{\sqrt{2}}}{2}$,则实数m等于( )
| A. | 2 | B. | 2或$\frac{8}{3}$ | C. | 2或6 | D. | 2或8 |