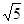题目内容
过双曲线的一个焦点F2作垂直于实轴的弦PQ,F1是另一焦点,若△PF1Q是钝角三角形,则双曲线的离心率e范围是( )
分析:根据△PF1Q是钝角三角形,可得∠PF1F2>45°,再利用通径,即可得出结论.
解答:解:由题意,∵△PF1Q是钝角三角形,
∴∠PF1F2>45°,
∴tan∠PF1F2=
>1,
∴PF2>F1F2,
∵过双曲线的一个焦点F2作垂直于实轴的弦PQ,
∴PQ=
,
∴
>2c,
∴c2-a2≤2ac,
∴e2-2e-1>0,
∵e>1,
∴e>
+1.
故选C.
∴∠PF1F2>45°,
∴tan∠PF1F2=
| PF2 |
| F1F2 |
∴PF2>F1F2,
∵过双曲线的一个焦点F2作垂直于实轴的弦PQ,
∴PQ=
| 2b2 |
| a |
∴
| b2 |
| a |
∴c2-a2≤2ac,
∴e2-2e-1>0,
∵e>1,
∴e>
| 2 |
故选C.
点评:本题主要考查了双曲线的简单性质,考查计算能力,确定∠PF1F2>45°是关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 的一个焦点F作它的一条渐近线的垂线FM,垂足为M并且交
的一个焦点F作它的一条渐近线的垂线FM,垂足为M并且交 轴于E,若M为EF中点,则
轴于E,若M为EF中点,则 =___________.
=___________. 的一个焦点F作一条渐近线的垂线,若垂足恰在线段
的一个焦点F作一条渐近线的垂线,若垂足恰在线段 (
( 为原点)的垂直平分线上,则双曲线的离心率为
.
为原点)的垂直平分线上,则双曲线的离心率为
. 的一个焦点F作其一条渐近线的垂线,若垂足恰在线段OF(O为原点)的垂直平分线上,则双曲线的离心率为( )
的一个焦点F作其一条渐近线的垂线,若垂足恰在线段OF(O为原点)的垂直平分线上,则双曲线的离心率为( ) C.
C. D.
D.
 的一个焦点F作一条渐近线的垂线,若垂足恰在线段
的一个焦点F作一条渐近线的垂线,若垂足恰在线段 (
( 为原点)的垂直平分线上,则双曲线的离心率为_______
___.
为原点)的垂直平分线上,则双曲线的离心率为_______
___. 的一个焦点F作一条渐近的垂线,垂足为点A,与另一条渐近线并于点B,若
的一个焦点F作一条渐近的垂线,垂足为点A,与另一条渐近线并于点B,若 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )  B.
B. C.2 D.
C.2 D.