题目内容
(1)若曲线C是双曲线,求k的取值范围;(2)若曲线C是焦点在x轴上的双曲线且离心率为![]() ,求此双曲线的方程;
,求此双曲线的方程;
(3)对于满足条件(2)的双曲线,是否存在过点B(1,1)的直线l,使直线l与双曲线交于M,N两点且B是线段MN的中点?若存在,求出直线l的方程;若不存在,请说明理由.
解:(1)当k=-1、k=0或k=![]() 时,曲线C表示直线.
时,曲线C表示直线.
当k≠-1且k≠0且k≠![]() 时,曲线C可化为
时,曲线C可化为 =1.①
=1.①
方程①表示双曲线的充要条件是![]() <0,解之得0<k<
<0,解之得0<k<![]() .
.
(2)∵曲线C是焦点在x轴上的双曲线且离心率为![]() ,∴a2=
,∴a2=![]() ,b2=
,b2=![]() ,从而有e2=
,从而有e2= =3,
=3,
∴k=1,
故曲线C的方程为x2-![]() y2=1.
y2=1.
(3)假设存在直线l,设M(x1,y1),N(x2,y2),则有
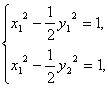 即x12-x22-
即x12-x22-![]() (y12-y12)=0,
(y12-y12)=0,
∴2(x1-x2)(x1+x2)=(y1-y2)(y1+y2).
∵B是线段MN的中点,
∴x1+x2=2,y1+y2=2,
∴直线l的斜率k=![]() =2,
=2,
即直线l:y=2x-1,
又直线l与双曲线交于MN两点,由 得2x2-4x+3=0,
得2x2-4x+3=0,
此时Δ=16-4×2×3=-8<0,方程无实数根.即直线l与双曲线x2-![]() y2=1无交点.
y2=1无交点.
故满足条件(3)的直线l不存在.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目