题目内容
东方旅社有100张普通客床，每床每夜收租费10元时，客床可以全部租出，若每床每夜收费提高2元，便减少10张床租出，再提高2元，又再减少10张床租出，依此变化下去，为了投资少而获利大，每床每夜应收取租金（ ）A．14元
B．16元
C．14元或16元
D．18元
【答案】分析：设每床每夜x元，收入为y，根据“若每床每夜收费提高2元，便减少10张床租出，”
建立获利函数模型：y=x×[100-10×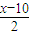
]=-5x2+150x，再由二次函数法研究最值及取得最值的状态．
解答：解：设：每床每夜x元，收入为y．（10≤x＜30）
∴y=x×[100-10×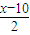
]
∴y=-5x2+150x=-5（x-15）2+1125
所以一百张床位的条件下每张床15元来的人最多．
若不存在提高一元的情况下，为了节省酒店的清洁电气等开支，
则人少的情况下较好，所以最为经济的是14或16元每夜每床．
故选C
点评：本题主要考查函数模型的建立和应用，对于利润类型要多注意其构成要素和使用范围．
建立获利函数模型：y=x×[100-10×
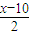]=-5x2+150x，再由二次函数法研究最值及取得最值的状态．解答：解：设：每床每夜x元，收入为y．（10≤x＜30）
∴y=x×[100-10×
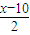]∴y=-5x2+150x=-5（x-15）2+1125
所以一百张床位的条件下每张床15元来的人最多．
若不存在提高一元的情况下，为了节省酒店的清洁电气等开支，
则人少的情况下较好，所以最为经济的是14或16元每夜每床．
故选C
点评：本题主要考查函数模型的建立和应用，对于利润类型要多注意其构成要素和使用范围．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目