题目内容
已知中心在原点,焦点在坐标轴上的双曲线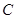 经过
经过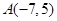 、
、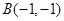 两点
两点
(1)求双曲线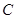 的方程;
的方程;
(2)设直线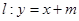 交双曲线
交双曲线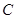 于
于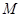 、
、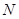 两点,且线段
两点,且线段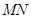 被圆
被圆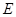 :
: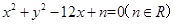 三等分,求实数
三等分,求实数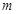 、
、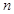 的值
的值
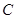 经过
经过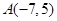 、
、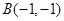 两点
两点 (1)求双曲线
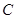 的方程;
的方程;(2)设直线
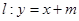 交双曲线
交双曲线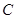 于
于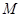 、
、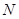 两点,且线段
两点,且线段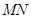 被圆
被圆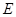 :
: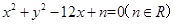 三等分,求实数
三等分,求实数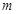 、
、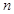 的值
的值 (1)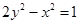 ;(2)
;(2)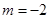 ,
,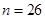
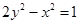 ;(2)
;(2)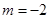 ,
,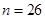
试题分析:(1)求双曲线
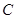 的方程,可设双曲线
的方程,可设双曲线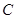 的方程是
的方程是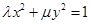 ,利用待定系数法求出
,利用待定系数法求出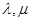 的值即可,由双曲线
的值即可,由双曲线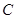 经过
经过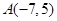 、
、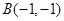 两点,将
两点,将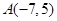 、
、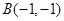 代入上面方程得,
代入上面方程得,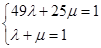 ,解方程组,求出
,解方程组,求出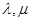 的值,即可求出双曲线
的值,即可求出双曲线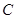 的方程;(2)求实数
的方程;(2)求实数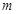 、
、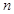 的值,直线
的值,直线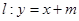 交双曲线
交双曲线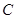 于
于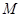 、
、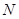 两点,且线段
两点,且线段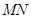 被圆
被圆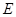 :
: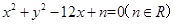 三等分,可知圆心与
三等分,可知圆心与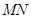 的中点垂直,设
的中点垂直,设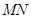 的中点
的中点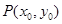 ,则
,则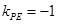 ,而圆心
,而圆心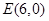 ,因此只需找出
,因此只需找出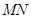 的中点
的中点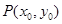 与
与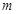 的关系,可将
的关系,可将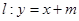 代人
代人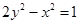 ,得
,得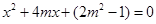 ,设
,设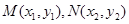 ,利用根与系数关系及中点坐标公式得
,利用根与系数关系及中点坐标公式得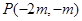 ,这样可求得
,这样可求得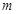 的值,由
的值,由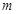 的值可求出
的值可求出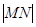 的长,从而得圆的弦长,利用勾股定理可求得
的长,从而得圆的弦长,利用勾股定理可求得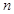 的值
的值 试题解析:(1)设双曲线
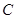 的方程是
的方程是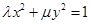 ,依题意有
,依题意有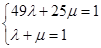 2分
2分解得
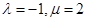 3分 所以所求双曲线的方程是
3分 所以所求双曲线的方程是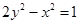 4分
4分(2)将
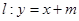 代人
代人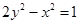 ,得
,得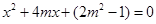 (*)
(*)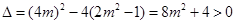 6分
6分设
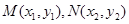 ,
,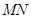 的中点
的中点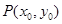 ,则
,则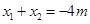 ,
,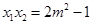 7分
7分则
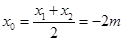 ,
,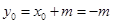 ,
,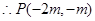 8分
8分又圆心
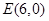 ,依题意
,依题意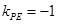 ,故
,故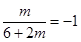 ,即
,即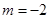 9分
9分将
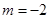 代人(*)得
代人(*)得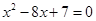 ,解得
,解得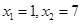
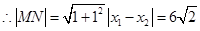 10分
10分故直线
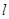 截圆
截圆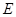 所得弦长为
所得弦长为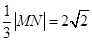 ,又
,又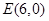 到直线
到直线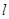 的距离
的距离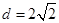 11分
11分所以圆
 的半径
的半径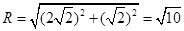
所以圆
 的方程是
的方程是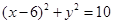 12分
12分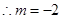 ,
,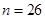 13分
13分
练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
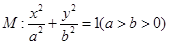 的离心率为
的离心率为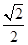 ,且经过点
,且经过点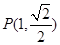 过坐标原点的直线
过坐标原点的直线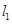 与
与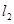 均不在坐标轴上,
均不在坐标轴上,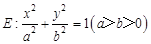 ,斜率为1的直线不经过原点
,斜率为1的直线不经过原点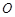 ,而且与椭圆相交于
,而且与椭圆相交于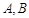 两点,
两点,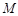 为线段
为线段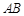 的中点.
的中点.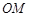 与
与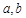 之间满足的关系式;若不能,说明理由;
之间满足的关系式;若不能,说明理由;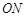 的中点,且
的中点,且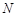 点在椭圆上.若
点在椭圆上.若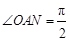 ,求
,求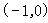 ,且离心率
,且离心率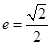 的椭圆
的椭圆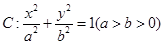 上下两顶点分别为
上下两顶点分别为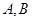 ,直线
,直线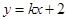 交椭圆
交椭圆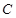 于
于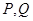 两点,直线
两点,直线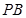 与直线
与直线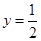 交于点
交于点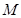 .
.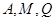 三点共线.
三点共线.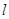 与椭圆
与椭圆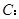
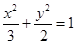 交于
交于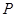
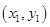 、
、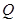
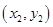 两不同点,且△
两不同点,且△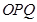 的面积
的面积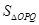 =
=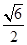 ,其中
,其中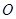 为坐标原点.
为坐标原点.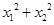 和
和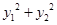 均为定值;
均为定值;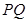 的中点为
的中点为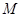 ,求
,求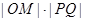 的最大值;
的最大值;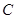 上是否存在点
上是否存在点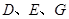 ,使得
,使得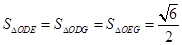 ?若存在,判断△
?若存在,判断△ 的形状;若不存在,请说明理由.
的形状;若不存在,请说明理由.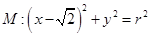
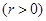 ,若椭圆
,若椭圆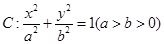 的右顶点为圆
的右顶点为圆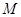 的圆心,离心率为
的圆心,离心率为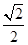 .
.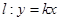 ,使得直线
,使得直线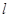 与椭圆
与椭圆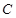 分别交于
分别交于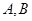 两点,与圆
两点,与圆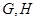 两点,点
两点,点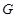 在线段
在线段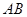 上,且
上,且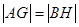 ,求圆
,求圆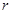 的取值范围.
的取值范围.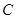 的顶在坐标原点,焦点
的顶在坐标原点,焦点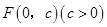 到直线
到直线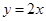 的距离是
的距离是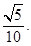
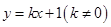 与抛物线
与抛物线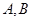 两点,设线段
两点,设线段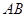 的中垂线与
的中垂线与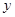 轴交于点
轴交于点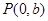 ,求
,求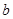 的取值范围.
的取值范围.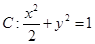 的左、右焦点分别为
的左、右焦点分别为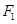 、
、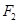 ,
,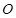 为原点.
为原点.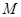 为椭圆
为椭圆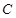 上的一点,
上的一点,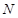 是
是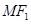 的中点,且
的中点,且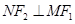 ,求点
,求点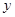 轴的距离;
轴的距离;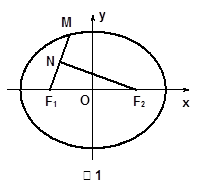
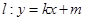 与椭圆
与椭圆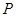 、
、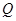 两点,若在椭圆
两点,若在椭圆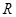 ,使四边形
,使四边形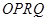 为平行四边形,求
为平行四边形,求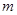 的取值范围.
的取值范围.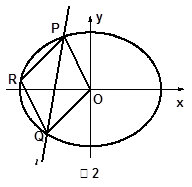
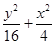 =1,椭圆C2以C1的短轴为长轴,且与C1有相同的离心率.
=1,椭圆C2以C1的短轴为长轴,且与C1有相同的离心率.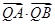 =4,求直线l的方程.
=4,求直线l的方程.